(2017)
Abstract: In his essay, “The Kalam Cosmological Argument: The Question of the Metaphysical Possibility of an Infinite Set of Real Entities,” Arnold T. Guminski presents his solution to the problem of counterintuitive absurdities, which he believes results from applying Cantorian theory to the real world. He calls his proposal an alternative version (AV) of the application of Cantorian theory to the real world. However, there are three serious problems with AV. First, it attempts to achieve by a priori methods what can only be accomplished by a posteriori means. Without empirical evidence, it specifies how a system of mathematics applies to the real world. Second, AV is far more radical than simply being an alternative way to apply Cantorian theory. In fact, it would require a non-Cantorian set theory, which raises the question of whether a set theory can be fully developed that is consistent with AV. And finally, AV is completely unnecessary, because the so-called counterintuitive absurdities that AV was devised to address are not absurdities at all.
In a second essay, “The Kalam Cosmological Argument Yet Again: The Question of the Metaphysical Possibility of an Infinite Temporal Series,” Guminski argues that it’s possible for time to have no beginning by showing that although any finite segment of time is formed by successive addition, the totality of all time need not be formed this way. His argument is essentially correct, and although he includes AV as an important part of it, it’s actually independent of AV.
Introduction
Knowledge of the Real World
Non-Cantorian Set Theory
Correspondence
Basic Concepts
Bijection
Other Correspondences
Infinite Sets
Counterintuitive Absurdities
Humans and Hands
Hilbert’s Hotel
Inches and Feet
Library with Infinitely Many Books
Absurdities Involving Time
Years Up Through a Particular Year
Tristram Shandy
The Central Issue
Infinite Temporal Series
Conclusion
Notes
Introduction
1. William Lane Craig is undoubtedly the leading proponent of the kalam cosmological argument (KCA), a variant of the cosmological argument for the existence of God. The second premise of KCA is that the universe has a beginning. Craig presents several arguments for this, including two that seek to show that a beginningless universe is metaphysically impossible. The first asserts that an actual infinite cannot exist because it would result in counterintuitive absurdities. The second asserts that time consists of a temporal series of events formed by successive addition, and any such series cannot be an actual infinite, even if it’s possible for other types of infinites to be real. The two essays by Arnold T. Guminski that are the subject of this paper were written to refute these two arguments. Regarding his essay on the first argument, Guminski writes, “This paper, as far as I am aware, is unusually (if not uniquely) different from others critical of the KCA in that I agree with Craig that counterintuitive absurdities are indeed generated by the application of Cantorian theory to the real world according to (what I call) the standard version.” (AG1.5)[1]
2. To paraphrase Guminski’s first example of a counterintuitive absurdity (AG1.15), consider a set of 100 people, each of whom has one head and two hands. It’s intuitively obvious there is a one-to-one correspondence between heads and people, but not between hands and people, which is instead a two-to-one correspondence. But if there are infinitely many people, set theory says there is a one-to-one correspondence between hands and people. Now this is not at all intuitively obvious. Moreover, there are still two hands attached to each person, so it’s intuitively obvious there is still a two-to-one correspondence of hands to people. Thus, according to Guminski, the one-to-one correspondence posited by set theory is a counterintuitive absurdity. Now the question is whether intuition can be reconciled with set theory. Craig’s answer is no, from which he concludes that it’s impossible for a real infinite to exist, although abstract infinites can exist in the conceptual world of pure mathematics. (AG1.4) Guminski’s answer is more nuanced. He argues that real infinites can exist provided they differ in some way from abstract infinites. In this case, the difference must allow the real infinite set of hands to have a two-to-one correspondence with the real infinite set of people even though the abstract infinite set of hands has a one-to-one correspondence with the abstract infinite set of people.
3. To accommodate this difference between real and abstract sets, Guminski presents what he calls an alternative version (AV) of the application of Cantorian theory to the real world. He says AV and the standard version (SV) are both essentially bridging rules, which “may be thought of as being in the nature of … metaphysical axiom[s].” (AG1.15). He gives AV in AG1.19 as a set of four propositions, which I have paraphrased here:
- AV1: There is a one-to-one correspondence between every real infinite and ℕ.[2]
- AV2: The cardinality of every real infinite is אo, which is the cardinality of ℕ.
- AV3: Even though any two real infinites have the same cardinality, they do not necessarily have a one-to-one correspondence with each other.
- AV4: No real infinite has a one-to-one correspondence with any of its infinite proper subsets.
4. Since Guminski is not a mathematician[3], AV is, in a way, very impressive. His intuitive insight into the problem is in some ways very keen. Unfortunately, it’s also naïve, by which I mean it has not been sufficiently shaped by mathematical experience. Ultimately, AV has three serious problems that make it impossible to accept: (1) It claims knowledge about the real world without empirical evidence, (2) it’s inconsistent with existing set theory and would require an alternative, non-Cantorian set theory, and (3) it’s completely unnecessary.
5. There is a fourth problem with AV that I mention here only in passing, namely the first two propositions of AV limit all real infinites to countable infinites. Guminski says this is “for purposes of convenience only” after giving two reasons why this is so, namely (1) “we have enough problems just talking about denumerable infinites,” and (2) Craig claims it’s metaphysically impossible for uncountable infinites to exist in the real world. (AG1.10) But these are merely reasons to avoid discussing the topic, when what’s needed is a justification for supposing uncountable infinites cannot exist since otherwise AV1 and AV2 cannot be true.
6. Ultimately, the problem with AV—and much of the debate that inspired it—is that it’s based on an insufficient understanding of the mathematics at the core of the debate. Consequently, much of this paper is devoted to filling in the gaps on the subject. Since this is intended for nonmathematicians, I have limited the math to a few basic features of set theory[4] and elementary algebra.[5]
Knowledge of the Real World
7. When Immanuel Kant first published his Critique of Pure Reason in 1781, he could claim with complete confidence that “All mathematical judgments, without exception, are synthetic,” and that “mathematical propositions, strictly so called, are always judgments a priori.”[6] In the nineteenth century, the development of non-Euclidean geometry and the axiomatic formulation of other branches of mathematics made it increasingly difficult to maintain the Kantian view that mathematics is both synthetic and a priori.[7] For centuries the difference between pure and applied mathematics was thought to be primarily a matter of exactness. In pure geometry, lines have no width and are perfectly straight, which of course is not the case with real lines. Moreover, while counting can be exact, measuring can only be approximate. There is always some margin of error. But this must be small for us to say the math applies. When the error is too great, we’re forced to concede the math ceases to describe the real world.
8. As our understanding of axiomatic systems grew, it became increasingly clear there is a more fundamental difference between pure and applied mathematics. A formalized axiomatic system has four components, namely (1) a set of symbols, (2) formation rules telling how symbols can be combined into valid formulas, (3) transformation rules for changing one formula into another, and (4) axioms, that is, a set of formulas that are true by fiat.[8] New theorems are derived by applying the transformation rules to the axioms or existing theorems. Any meaning assigned to the symbols “plays no essential role in the process of deriving theorems.”[9] Consequently, the symbols have no inherent meaning. This, combined with the fact that statements (i.e., formulas) are true only by convention, led to Bertrand Russell’s pungent quip that “mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true.”[10]
9. When meaning is assigned to the symbols (and thence to the formulas), that meaning constitutes a model for the system. For example, in the propositional calculus, some symbols are variables, and others are connectives used to combine variables into formulas. In the standard model for the propositional calculus, variables are interpreted as propositions, which have truth values. But by assigning a different meaning to the symbols, the system can be applied to a completely different model. For example, in a computer chip, the variables are circuits and their truth values are distinct voltage levels, while logic gates are used to combine variables.[11] A formalized axiomatic system is obviously analytic and a priori, and as such is part of pure mathematics. When a model is specified for an axiomatic system and that model is part of the real world, then the question arises whether the system accurately describes the model. This is an empirical question, rendering the system (as applied to the model) synthetic, a posteriori, and part of applied mathematics.
10. The Kantian view was dealt another blow by the theory of relativity. As Einstein wrote, “our previous discussion … is sufficient to exclude the possibility of the exact validity of Euclidean geometry in our universe. But it is conceivable that our universe differs only slightly from a Euclidean one … Such a universe might fittingly be called a quasi-Euclidean universe … [But this] would present to us … [a previously described] unsatisfactory picture … [and so] the universe cannot be quasi-Euclidean.”[12] Bertrand Russell summed up the situation: “Thus of the two kinds of geometry one [pure geometry] is a priori but not synthetic, while the other [geometry as a branch of physics] is synthetic but not a priori.”[13]
11. So what are we to make of bridging rules that purport to tell us how to apply mathematics to the real world? Guminski quotes Craig as saying, “Cantor’s system and set theory are concerned exclusively with the mathematical world, whereas our argument concerns the real world.” Guminski then adds, “It is thus necessary to devise appropriate bridging (or correspondence) rules in order to apply such theory to the real world. What one must bear in mind is that the bridging rule, whereby a pure mathematical theory of transfinite numbers is rendered applicable to a real world, is not itself part of that theory whether as a theorem or otherwise.” (AG1.15) Guminski’s argument would have benefited greatly had he presented some examples of bridging rules in other areas of mathematics. For example, what bridging rule allows us to apply 1 + 1 = 2 to the real world?[14] More to the point, why do we need a bridging rule at all?
12. To apply 1 + 1 = 2 to the real world, first it’s necessary to specify a model, then to show the math accurately describes it. If the model consists of countable things—for example, apples—then we can show that one apple plus one apple equals two apples. But if the model consists of things that are measured rather than counted, then we may find the math does not apply consistently. For example, one liter of water plus one liter of water equals two liters of water (as accurately as we can measure anyway), but one liter of air plus one liter of air will have whatever volume the container has, which may be drastically different from two liters. Finding evidence is an inductive process. Successfully testing a model doesn’t prove the math will always apply in that model. However, a single failure may be sufficient to show the math does not apply to that model.
13. Axiomatic set theory, by virtue of being axiomatic, belongs to pure mathematics. In it, sets are abstractions. But it can be applied by choosing an appropriate model, which can be almost anything that can be counted. There can be sets of dogs, cars, or planets, for example, because these things can be counted. On the other hand, things that can’t be counted—such as water, love, or democracy—generally cannot be used as a model. But there is ample empirical evidence that set theory can be successfully applied to a number of models—at least for finite sets.
14. To apply those elements of set theory relating to infinite sets to the real world, we need to specify a model and then find empirical evidence that set theory applies to that model. Of course, there is a fundamental problem, namely the lack of a real infinite set to use as a model. This is not to say there is no such real set, only that there is no general agreement that one exists. If there were, someone would have pointed to it by now and said, “See! Craig is obviously wrong to say no such set can exist.” But without such a real set, how can we test any claims about how—or even whether—to apply the mathematics of such sets? Hypothetical sets are of no value because we can’t obtain empirical evidence from them.
15. Since I am arguing that there is no empirical evidence to support either Craig’s or Guminski’s version of how real infinite sets behave, I must also admit there is none to support any version that I endorse. So I need to be clear about my position. I don’t know how real infinite sets behave or even if they exist, nor does anyone else. But Cantorian theory is the only well-developed set theory we have. It accurately describes real finite sets, and, as I will show, there is no convincing argument that it fails to describe real infinite sets. Consequently, the most reasonable position is to tentatively assume that Cantorian theory—without changes and without bridging rules—does apply to real infinite sets, if there are any.
16. Intuition undoubtedly plays an important role in mathematics, but in no sense can it be considered an arbiter of truth. In pure mathematics, truth is based on proof, and the accepted basis for proof in all branches of mathematics is the axiomatic method.[15] In applied mathematics, and science in general, truth is based on empirical evidence. Thus the fact that an assertion is counterintuitive doesn’t mean that it’s false, let alone absurd, and this is especially true when we lack any experience with what is being asserted. Neither Craig nor Guminski disputes anything in pure mathematics, nor can they provide the empirical evidence required by applied mathematics. There is little left for them to appeal to other than intuition. Since intuition depends on experience, and our experience does not include real infinite sets, it is questionable at best to suppose intuition can provide any real insight into the subject, especially when it contradicts established mathematics.
17. In an appendix, Guminski discusses the idea of a first philosophy, which provides some set of principles that underpin all knowledge, or at least all knowledge of the real world. For my part, I do not subscribe to a first philosophy in this sense. I believe it’s based on the mistaken belief that induction is a special form of deduction, and thus subject to the same types of errors. The view I object to is clearly stated in a quotation Guminski gives from C. D. Broad: “All inductions make some assumption about the structure of nature, which may be called the ‘Uniformity of Nature,’ for want of a better name. It would evidently be circular to try to prove such a proposition inductively.” (AG2.56) I would argue that circular reasoning occurs only in deduction. In contrast, induction—at least in the long term—is self-correcting.[16] I would go even farther and say that necessity is also a property of deductive logic and not the real world, except insofar as deductive logic describes the real world. So, unlike Guminski and Craig, I would say the phrase metaphysically necessary can mean nothing more than logically necessary.[17] I leave it to the reader to decide to what degree, if any, my differences with Guminski on these points prejudice the argument I make in this section. I am confident these differences are irrelevant in the remaining sections of this paper. Guminski claims that the propositions of AV are metaphysically necessary and they have “a higher epistemic status than those of SV, taken as a whole.” (AG1.20) But these are a priori assertions when only a posteriori evidence can lead us from pure to applied mathematics.
Non-Cantorian Set Theory
18. As an axiomatic system, Euclidean geometry belongs to pure mathematics. To use it as applied mathematics, we need a model and empirical evidence. The model, of course, is the actual space we live in and its contents. To get empirical evidence, we need to measure things. For example, in Euclidean geometry the sum of the angles in a triangle is 180°. When we measure the angles of real triangles, we generally find they add up to 180° within the tolerances of our measuring instruments. But this may not be the case in relativistic situations, that is, situations where Newtonian physics ceases to apply and Einstein’s theory of relativity is required. What do we do when the empirical evidence fails to support the hypothesis that the axiomatic system describes the selected model? In the previous section I quoted Einstein as saying space cannot be Euclidean because it differs significantly from the abstract space of Euclidean geometry. In other words, the axiomatic system (Euclidean geometry) does not apply to the model (actual space), at least not in relativistic situations. Consequently, whatever geometry does apply is non-Euclidean.
19. Now if we ask whether the empirical evidence shows that Cantorian[18] theory (the axiomatic system) describes real infinite sets (the selected model), we’re immediately stymied because we have neither a model nor empirical evidence. But for the sake of argument, suppose we have both, and the empirical evidence contradicts the hypothesis that Cantorian theory applies to real infinite sets. Specifically, suppose we have evidence that equipollence is not transitive for real infinite sets. Since the transitivity of equipollence is a theorem in Cantorian theory, and the (hypothetical) evidence shows this isn’t true for real infinite sets, then we ought to conclude that Cantorian theory does not apply to real infinite sets, and whatever set theory does apply is non-Cantorian.[19]
20. But Guminski has chosen a different approach. He says, “I propose that the relation of equipollence of each of two real infinites with N is not transitive with respect to another real infinite.” (AG1.24) This is a direct consequence of AV4, which says that “no real infinite is equipollent with any of its infinite proper subsets, although both have the same cardinality.” (AG1.19) He tells us that AV4 is a bridging rule, and as such it is not part of Cantorian theory, but merely tells us how to apply Cantorian theory to the real world. But how is this possible when AV4 contradicts Cantorian theory?
21. Suppose there is an axiomatic system of arithmetic (let’s call it Goofian arithmetic) in which 1 + 1 = 3.[20] If we try to apply Goofian arithmetic to the real world, we find it’s contradicted by the empirical evidence. The reasonable conclusion is that it doesn’t apply, and whatever does apply is non-Goofian. So why would we invent a bridging rule that says when applying Goofian arithmetic to the real world, change 1 + 1 = 3 to 1 + 1 = 2? Since we wind up with 1 + 1 = 2 whether we use non-Goofian (i.e., ordinary) arithmetic or the bridging rule, why does it matter? Consider that this is just one statement in Goofian arithmetic. How many more bridging rules will we need for all the other statements that don’t match reality? Since 1 + 1 = 3 is probably a very basic theorem (if not an axiom) in Goofian arithmetic, it seems likely we will need a great many more. Similarly, the transitivity of equipollence is also fundamental, and it cannot be dropped without significantly changing set theory in ways that make it inconsistent. Indeed, Guminski tells us to “be prepared to consider the possibility that the mathematical properties of real infinites may radically differ in some respects from those of infinite sets of abstract entities”? (AG1.18) Consider some of the ways in which AV is inconsistent with Cantorian theory:
- Guminski points out that an infinite set is defined by being equipollent to one of its proper subsets (AG1.11). Since AV4 explicitly asserts that this never happens with real infinite sets, that means there can be no real infinite sets. The only way to avoid this is to redefine what it means for a set to be infinite.
- AV3 says that two real infinite sets can have the same cardinality without being equipollent. But having the same cardinality means the same thing as being equipollent. Both are defined as having a one-to-one correspondence between the two sets.[21] Thus AV3 is self-contradictory unless either cardinality or equipollence is redefined.
- In Cantorian theory, a one-to-one correspondence is defined as a bijection, or bijective function. (I will explain in the next section what makes a function bijective.) A consequence of this definition is that equipollence is transitive. That makes AV4 inconsistent with AV1 unless a one-to-one correspondence is redefined.[22]
22. All these problems require a redefinition of terms. But redefining a term invalidates any statement using that term. It would be like saying the word parallel in pure geometry refers to two coplanar lines that don’t intersect, but in the real world, it refers to two lines that may or may not meet. The truth of any statement using the word parallel would be in doubt when applied to the real world.
23. Now consider Guminski’s statement of the bridging rule posited by SV: “[I]f two real infinites A and B are each equipollent to N (the set of all natural numbers), then they are necessarily equipollent to each other, and such equipollence is the necessary and sufficient condition for both having one and the same cardinal number.” (AG1.15) But these are precisely the criteria Guminski uses to identify Cantorian theory. (AG1.F10) So SV says nothing more than to apply Cantorian theory as is, which is the same as having no bridging rule at all.
24. Guminski claims AV “cannot be proved to be inconsistent or invalid in a non-question-begging way (e.g., by stipulating that SV is true).” (AG1.20) Even if AV is internally consistent, it’s clearly inconsistent with Cantorian theory. But what if Guminski were to accept this and say that real infinite sets are described by a non-Cantorian set theory? This would eliminate all the problems I’ve discussed in this section. It would also obviate the need for his bridging rules, since they would be theorems in this non-Cantorian set theory. The only impediment to this option is the fact that no one has yet developed a non-Cantorian set theory, let alone one that includes the bridging rules from AV as theorems.
25. Suppose someone were to develop a non-Cantorian set theory. The development of non-Euclidean geometry began by changing Euclid’s parallel postulate and then deducing new theorems that were a consequence of this change. Nothing about the result could be assumed in advance. Similarly, the development of a non-Cantorian set theory would have to begin by changing one or more axioms and deducing new theorems from them. But that means there’s no guarantee that the bridging rules from AV would be theorems, because the result can’t be known in advance. So unless someone actually develops a non-Cantorian set theory compatible with AV, we can’t know whether it’s even possible.
26. But assuming someone did develop a non-Cantorian set theory compatible with AV, how would we know if it applied to real infinite sets? Without empirical evidence, we would have no way of knowing which set theory—Cantorian, non-Cantorian, or neither—best describes real infinite sets. However, there are two factors that could incline us one way or the other. Since Cantorian theory accurately describes real finite sets, if the non-Cantorian did not, we would probably think Cantorian theory to be more likely to describe real infinite sets as well. On the other hand, if Guminski is correct that Cantorian theory would result in counterintuitive absurdities if it were applied to real infinite sets, this would make non-Cantorian set theory the better candidate.
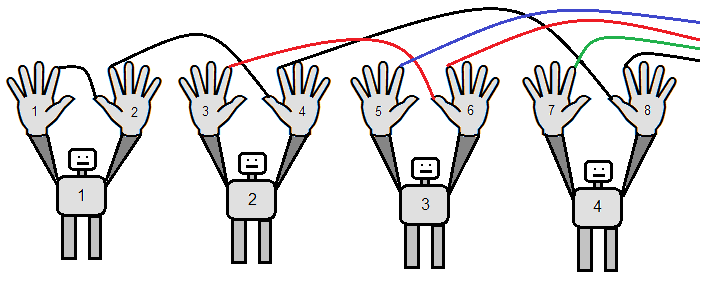
27. Clearly any set theory that is compatible with AV would be radically different from what Guminski calls Cantorian theory. What’s not clear is what such a non-Cantorian set theory would look like, let alone whether such a set theory could be internally consistent and still apply to the real world. Absent a developed non-Cantorian set theory compatible with AV, any claims that AV applies to the real world are premature.
Correspondence
Basic Concepts
28. The third problem with AV is that it attempts to solve a nonexistent problem, namely the notion that a real infinite would result in counterintuitive absurdities according to SV. To see why this is not so, it will be helpful to start with some basic ideas about correspondence. Consider the following three sets:
A = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 }
B = { 2, 4, 6, 8, 10, 12 }
C = { 1, 3, 5, 7, 9, 11 }
29. These definitions of A, B, C will remain effective until the section on infinite sets. These sets have the following properties:
- B ⊂ A (B is a subset of A.)
- C ⊂ A (C is a subset of A.)
- B ∩ C = ∅ (The intersection of B and C is the empty set, that is, they’re disjoint.)
- B ∪ C = A (The union of B and C is A.)
30. The most intuitive and natural way to map (or pair up) the elements of B with the elements of A is to map each element of B to itself. This correspondence is defined by the following function and its inverse. Below that is an arrangement of the two sets that expresses the mapping by vertically aligning the corresponding elements.
Correspondence 1:
Function: a = ƒ(b) = b
Inverse: b = g(a) = a
A: 1 2 3 4 5 6 7 8 9 10 11 12 B: 2 4 6 8 10 12
31. For the function ƒ, lowercase b is any arbitrary element of the set B, and lowercase a is the corresponding element of the set A. The domain of f is B and the codomain is ℕ. The image is the subset of A consisting of the function values. This is the subset of even numbers, which is the same as B. That means that half the elements of A, namely the odd numbers in C, are not paired with any element of B.
32. For the inverse function g, the domain is A, the codomain is ℕ, and the image is a superset of B, that is, some elements (the odd numbers again) are paired with numbers that are not elements of B. Since ƒ and g are each the inverse of the other, it’s arbitrary which is called the function and which the inverse. The function ƒ tells which element of A corresponds to any given element of B. The function g, on the other hand, tells which element of B (if any) corresponds to any given element of A.
33. The single most important thing to understand about this or any correspondence is that it’s a function and not any physical connection between the corresponding elements of two sets. Moreover, a function is not necessarily an equation. It can be any kind of algorithm, that is, a rule for identifying which element of the codomain corresponds to any given element of the domain. Whenever I refer to a physical arrangement of corresponding elements, I say it expresses the correspondence. The following table shows how I use these terms in this paper.
| Term | Meaning |
|---|---|
| correspondence | A function—which is a formula, algorithm, or rule for mapping each element of the domain to a specific element of the codomain—along with its inverse function (if any). |
| expressed correspondence | A physical representation or embodiment of a correspondence. |
34. It’s also important to understand that the existence of a particular correspondence between two sets does not preclude the existence of other correspondences between them. Consider the following additional correspondences between A and B and arrangements that express them. Different arrangements express different correspondences and vice versa.
Correspondence 2:
Function: a = ƒ(b) = b – 1
Inverse: b = g(a) = a + 1
A: 1 2 3 4 5 6 7 8 9 10 11 12 B: 2 4 6 8 10 12
Correspondence 3:
Function: a = ƒ(b) = b⁄2
Inverse: b = g(a) = 2a
A: 1 2 3 4 5 6 7 8 9 10 11 12 B: 2 4 6 8 10 12
Correspondence 4:
Function: a = ƒ(b) = b⁄2 + 6
Inverse: b = g(a) = 2(a – 6)
A: 1 2 3 4 5 6 7 8 9 10 11 12 B: 2 4 6 8 10 12
35. There are a great many other ways to pair up the elements of A and B, but no matter how we do it, we cannot pair all the elements of A with the elements of B without at least some of the elements of B being paired with more than one element of A. And the reason is obvious: A has more elements than B.
Bijection
36. If we pair up the elements of B and C, then we can create a mapping where every element of each set corresponds with exactly one element of the other set, as shown in Correspondence 5.
Correspondence 5:
Function: c = u(b) = b – 1
Inverse: b = v(c) = c + 1
B: 2 4 6 8 10 12 C: 1 3 5 7 9 11
37. The functions u and v are called bijections or bijective functions because they meet the following criteria:[23]
- Every element of B is paired with an element of C.
- No element of C is paired with more than one element of B.
- Every element of C is paired with an element of B.
- No element of B is paired with more than one element of C.
38. A bijective function defines a one-to-one correspondence between the set that is the domain of the function and the set that is its image. Every bijective function has an inverse that is also bijective. Strictly speaking, u meets the first two criteria and v meets the other two. In the first four correspondences, ƒ also meets the first two criteria (if we replace C with A in the criteria), while g meets the fourth criterion but not the third. In contrast, the function h defined below for Correspondence 6 meets the third criterion, but not the fourth.
39. Whether a function is bijective depends on not just the algorithm or formula for the function, but also the domain of the function and the domain of its inverse. If elements are added to or removed from either B or C, the function for Correspondence 5 is no longer bijective.
Other Correspondences
40. Guminski uses the term two-to-one correspondence in several places, but he never defines it, presumably because he assumes its meaning is obvious. Certainly in the case of finite sets, everyone knows what he means. For example, A has a two-to-one correspondence with B because it has twice as many elements. More generally we could say a set X has an n-to-one correspondence with a set Y if the cardinality of X is n times the cardinality of Y. But while this is true, it’s not a heuristically useful definition. To define the two-to-one correspondence of A to B, we could try using a function like Correspondence 6:[24]
| Function: b = h(a) = | { | a, if a is even |
| a + 1, if a is odd | ||
| Inverse: none |
A: 1 2 3 4 5 6 7 8 9 10 11 12 / / / / / / B: 2 4 6 8 10 12
41. This maps every element of A to an element of B, but there is no inverse function to map each element of B to two elements of A because a function, by definition, has only one output for any given input. Without an inverse function, we need some other way to guarantee that every element of B is mapped to exactly two elements of A.
42. What is needed to define an n-to-one correspondence is the concept of a partition. To partition a set means to split it into subsets so that every element is in exactly one subset.[25] For example, A can be partitioned into B and C. As another example, one way B itself can be partitioned is by splitting it into these 3 subsets: { 2, 4, 8 }, { 10 }, and { 6, 12 }. Each element of B is in one and only one of these subsets. On the other hand, the subsets { 2, 6, 10 } and { 8, 10, 12 } do not form a partition of B for two reasons, namely (1) the element 4 is not in any subset, and (2) the element 10 is in more than one.
43. The concept of a partition can be used to say a set X has an n-to-one correspondence with a set Y if and only if X can be partitioned into n subsets, each of which has a one-to-one correspondence with Y. For example, if X has twelve elements and Y has three, then X can be partitioned into four subsets of three elements each. Each of these four subsets then has a one-to-one correspondence with Y, hence X has a four-to-one correspondence with Y. When dealing with finite sets, partitioning bears some similarity to division. But division is undefined for infinite sets, so partitioning is used instead.
44. Applying this to Correspondence 6, A can be partitioned into two subsets, namely B and C. Now B has a one-to-one correspondence with itself and with C, therefore A has a two-to-one correspondence with B. This means (1) the correspondence is defined by two bijective functions, one for each subset in the partition, and (2) A cannot have an n-to-one correspondence with B for any value of n other than 2.
45. Before moving on to infinite sets, I want to look at the meaning of the word more. We can say that A has more elements than B because the cardinality of A is greater than the cardinality of B. But it’s sometimes possible to know that one set has more elements than another even if we don’t know the cardinality of either set. In particular, if B is a proper subset of A, then A has more elements than B. This is true because every element that’s in B is also in A, but A has at least one other element that is not in B. Let’s use the words numerically and compositionally to distinguish these two cases, as shown in the following table. For finite sets, having compositionally more elements entails having numerically more elements.
| Term | Meaning |
|---|---|
| A has numerically more elements than B. | The cardinality of A is greater than the cardinality of B. |
| A has compositionally more elements than B. | B is a proper subset of A. |
Infinite Sets
46. Now let’s expand our definitions of sets A, B, and C from above to make them infinite sets. A is now the set of all natural numbers[26], B is the set of all even natural numbers, and C the set of all odd natural numbers. These new definitions of A, B, C will remain effective for the rest of this section. Correspondence 1 then becomes Correspondence 7, shown here:
Correspondence 7:
Function: a = ƒ(b) = b
Inverse: b = g(a) = a
A: 1 2 3 4 5 6 7 8 9 10 11 12 ... B: 2 4 6 8 10 12 ...
47. The only difference between Correspondences 1 and 7 is the change in the domain of the function and the domain of its inverse. This is illustrated in the partial expression of Correspondence 7 by the addition of ellipses to show the sequences continue indefinitely. The functions that pair up the elements of the two sets are still defined by the same formulas, and an infinite number of the elements of A (namely the odd numbers) are still not paired with an element of B. I said “an infinite number of the elements” rather than “half the elements” because half implies division, which is not defined for infinite sets.
48. Similarly Correspondence 2 and Correspondence 5 become Correspondence 8. I combined them to facilitate the discussion in the next paragraph.
Correspondence 8:
Function: a = ƒ(b) = b – 1
Inverse: b = g(a) = a + 1
Function: c = u(b) = b – 1
Inverse: b = v(c) = c + 1
A: 1 2 3 4 5 6 7 8 9 10 11 12 ... B: 2 4 6 8 10 12 ... C: 1 3 5 7 9 11 ...
49. Other than the fact that two correspondences have been combined, the only displayed difference is the addition of the ellipses. It should be apparent that u is still bijective[27], so there is a one-to-one correspondence between B and C. It should also be clear that A can be partitioned into B and C, and since B and C each have a one-to-one correspondence with themselves and each other, A has a two-to-one correspondence with B, as well as a two-to-one correspondence with C, exactly as one would intuitively assume.
50. When we convert Correspondence 3 to Correspondence 9, there is a significant change. Where before there were no elements in B corresponding to the numbers greater than 6, now there are. And because the supply of numbers in both sets is inexhaustible, there is a number in B to correspond with every number in A.
Correspondence 9:
Function: a = ƒ(b) = b⁄2
Inverse: b = g(a) = 2a
A: 1 2 3 4 5 6 7 8 9 10 11 12 ... B: 2 4 6 8 10 12 14 16 18 20 22 24 ...
51. The functions ƒ and g still have the same formulas, but now they’re bijective functions. Thus there is a one-to-one correspondence between A and B. Does this contradict the fact that A also has a two-to-one correspondence with B (shown in Correspondence 8), as it would if A and B were finite? Before answering that, look at Correspondence 10, which suggests that B has a three-to-one correspondence with A.
Correspondence 10:
Function and Inverse: The three-to-one correspondence requires three bijective functions.[28]
A: 1 2 3 4 ... / | / | / | / | B: 2 4 6 8 10 12 14 16 18 20 22 24 ...
52. In fact, any infinite set can be put into an n-to-one correspondence with any other infinite set of the same cardinality for any positive integer n. This is consistent with the cardinal number of the first set being n times the cardinal number of the second set because n × אo = אo for any positive finite value of n, and similarly for any other infinite cardinal number, not just אo. But we don’t need to stop with finite numbers. Any infinite set can be put into a אo-to-one correspondence with any other infinite set of the same cardinality. After all, אo × אo = אo. Far from being a contradiction, having infinitely many correspondences is a feature of infinite sets. But a particular arrangement expresses only one correspondence.
53. Infinite sets also have the following features:
- An infinite set can have the same cardinality as one of its proper subsets. In this case, B is a proper subset of A. Consequently, A has compositionally more elements than B, but not numerically more since they have the same cardinality.
- Whenever an infinite set is put in a one-to-one correspondence with one its proper subsets, there must be infinitely many elements that do not correspond with themselves[29], which is illustrated in Correspondence 9.
54. Later it will be helpful to remember Correspondence 11, which is derived from Correspondence 4.
Correspondence 11:
Function: a = ƒ(b) = b⁄2 + 6
Inverse: b = g(a) = 2(a – 6)
A: 1 2 3 4 5 6 7 8 9 10 11 12 ... B: 2 4 6 8 10 12 ...
55. Again the only displayed change is the addition of the ellipses. But here there is no n-to-one correspondence for any value of n. Every element of B is paired with an element of A, but A has 6 elements that are not paired with any element of B. It should be obvious that the number 6 in these functions is arbitrary. Thus there is a correspondence with any arbitrary number of elements of A not paired with an element of B (or vice versa). And as Correspondence 7 shows, the number of unpaired elements can be infinite.
56. Let A’ = { 7, 8, 9, … }. If we replace A with A’ in Correspondence 11 (which amounts to removing the first 6 elements from A), then the function becomes bijective. Changing the domain of the function or (as in this case) its inverse can change whether it’s bijective or not.
Counterintuitive Absurdities
Humans and Hands
57. With this background, we can now address the so-called counterintuitive absurdities. Let’s begin with the first example Guminski gives, namely the correspondence of an infinite number of humans with their hands. (AG1.15) Guminski says the one-to-one correspondence between humans and their pairs of hands is inconsistent with having a one-to-one correspondence between humans and their individual hands. In AG1.25 he specifically says the two-to-one correspondence of all hands to humans is inconsistent with a one-to-one correspondence of all hands to humans. When such a correspondence was pointed out to him, he rejected it on the grounds that all but one human would be paired with someone else’s hand, saying it was “patently inconsistent with the supposition that every human has exactly two hands, such that the sequence should be [each] human … is matched with both his hands.” (AG1.F28)
58. Of course Guminski is correct that the physical makeup of humans expresses a two-to-one correspondence of all hands to humans. But why does he believe this is inconsistent with a one-to-one correspondence? My guess is that he assumes a one-to-one correspondence would mean that each human would have only one hand, and this is inconsistent with each human having two hands. And it’s true that simultaneously having two hands and only one hand is inconsistent. But suppose we remove the word simultaneously. Since changing the makeup of humans would be problematic (ethically and logistically, but not logically), let’s change them to robots so we can remove all their hands and reattach them, but giving only one hand to each robot. Some robots would get a left hand, and some a right hand. But would we run out of robots before we ran out of hands? Of course not, because there is an endless supply of both.[30] The arrangement would now express the one-to-one correspondence. This raises two questions, to which I’ve added a third because it’s convenient to answer all three together.
- If a one-to-one correspondence is expressed, does that necessarily mean that each human (or robot) would have only one hand?
- A two-to-one correspondence and a one-to-one correspondence can be expressed at different times, but is it possible to express both at the same time?
- Is it possible, contrary to AV4, to express a one-to-one correspondence between a real infinite set and one of its proper subsets? Specifically, is it possible to express a one-to-one correspondence between the set of all robot hands and the set of just left hands?
59. To answer these questions, imagine a string tied to each pair of corresponding hands, where one hand is an element of the set of all hands and the other is an element of the set of just left hands. This is shown for the first four robots in Figure 1. (The use of different colors for the strings is not meant to signify anything. It just makes it easier to differentiate one string from another.) Every hand, including left hands, has a string tied to its index finger, but only left hands have strings on their thumbs. Thus the strings express the one-to-one correspondence between all hands and just left hands. This answers question 1 in the negative and question 3 in the affirmative. The arms still express the two-to-one correspondence of all hands to robots. Two different physical connections allow two different correspondences to be expressed simultaneously. Also, the end of the string that’s tied to the thumb of a left hand could have been tied instead to the head of the robot that the left hand is connected to. The strings would then express the one-to-one correspondence between all hands and robots while the arms express the two-to-one correspondence. This answers question 2 in the affirmative. It also illustrates the transitivity of equipollence.
Figure 1: Correspondence of All Hands to Left Hands:
60. It’s important to understand that the one-to-one correspondence between all hands and just left hands exists even if they are not tied together with strings. The correspondence exists not because it’s expressed by a physical connection between corresponding elements, but because there is a function defining the correspondence, that is, there is an algorithm or rule telling which elements to connect.
61. Imagine Ty has been assigned the task of attaching all these strings, and suppose Ty performs his task on each robot in order. Then on each robot he attaches three strings: Two new strings, one to the index finger on each hand, and one old string to the thumb of the left hand. So at any point, after attaching the strings to a particular robot, only half the strings he’s attached so far are attached at both ends. This is illustrated in Figure 1 where, after completing the fourth robot, he’s attached eight strings, but only four of them are attached to both an index finger and a thumb. The other four are attached only to an index finger. By the time these are all attached, he will have added twice as many new strings still left unattached to a thumb. But although the number of strings with only one end attached keeps growing larger and larger, each one of them will eventually be attached at both ends. Moreover, each one of them will be attached within a finite amount of time measured from when Ty starts with the first robot. Yet the amount of time Ty will spend on the entire task is infinite.[31] Since the process cannot be completed in a finite amount of time, the big question is: Does this mean (1) it can be completed in an infinite amount of time, or (2) it can never be completed? The answer to this question must wait until later in this essay.
62. But let’s go back to infinitely many humans for a moment. Suppose every human has one dollar, and suppose everyone gives that dollar to the person with the corresponding hand. Since everyone has two hands, that means everyone will get two dollars. Did we just magically double the amount of money in the universe? Of course not. All we’ve really done is change the correspondence that’s expressed by the physical arrangement of dollars and humans. There are no more dollars—either numerically or compositionally—than before. If we were to print infinitely many more dollars, then we would have compositionally more dollars, but not numerically more. Given an infinite number of dollars and people, we could distribute the dollars so that everyone gets an equal share amounting to any value we choose: one dollar, two dollars, a million dollars, or even infinitely many dollars per person. Conversely, we could distribute the dollars so that each dollar is shared by any number of people, including infinitely many people. When this stops seeming strange to you, then you’re beginning to understand how infinite numbers behave. But to truly understand, you have to realize that each possible correspondence is simply a function that maps dollars and people together.
Hilbert’s Hotel
63. Another alleged absurdity is Hilbert’s Hotel[32] (AG1.41), which has an infinite number of rooms, all of which are occupied. Now if another guest shows up, a room can be freed up by having the current occupant of each room move to the room with the next higher room number. Because there is no highest room number, every guest will have a room to move to. Craig objects because initially all the rooms are occupied and therefore there is no more room. This is an application of a general principle Craig lays down “that a new member cannot be added to a real infinite because its members, prior to any addition, already correspond one-to-one to N. Craig argues that N has been already completely exhausted or used up, in the sense of thereby precluding the addition of another member. Craig rightly contends that it is not sufficient to answer that the members of the augmented set can be reassigned numerals in order to take the addition of new members into account. Nevertheless, Craig is mistaken in his basic view.” (AG1.29) Guminski goes on to explain—quite correctly—that Craig is mistaken because the existence of a set X that is equipollent to ℕ does not preclude the existence of a proper subset or superset of X that is also equipollent to ℕ.
64. Guminski does not, however, explain why he agrees with Craig that reassigning numbers won’t work. I can only assume it’s because he accepts Craig’s reasoning. Craig’s argument[33] concerns adding a new book to an existing collection. If there are 100 books in the collection, numbered 1 through 100, and a new one is to be added with the number 1, the existing books could be renumbered by adding 1 to each book’s current number. But this would require using a previously unused number, namely 101. Now if there are infinitely many books, then, according to Craig, it would be impossible to renumber them because there are no unused numbers. But of course this reasoning is fallacious. In the finite collection, a previously unused number is needed because there is one book, namely the last, for which the next number is not currently in use. For all the other books in the collection, the next number is already in use (but about to be freed up) so an unused number is not needed for them. In the infinite collection, there is no book for which the next number is not currently in use, and thus there is no need for a previously unused number for any of them.
65. Guminski has another reason for regarding Hilbert’s Hotel as an absurdity (given SV). In AG1.26 he says that if A and B are real infinite sets that are equipollent, and n elements are added to A, then A and B are no longer equipollent. This is illustrated by Correspondence 11 above if we start with A’ and then change it to A. This change amounts to adding 6 new elements (the numbers 1 through 6) to A’. The function that defines Correspondence 11 is bijective for A’ and B, but not for A and B. Applying this to Hilbert’s Hotel, Guminski argues that if any new guests are added, “there would no longer be, according to AV, an equipollence between the rooms and the guests.” (AG1.41) He’s half right. The function that defines Correspondence 11 ceases to be bijective when new elements are added to A’, and therefore that correspondence is no longer one-to-one. However, the function that defines Correspondence 9, which is not bijective for A’ and B, is bijective for A and B, so that correspondence becomes one-to-one. So it’s not true that there is no longer an equipollence between the rooms and the guests. It’s just that the equipollence is now a different function, that is, a different correspondence.
66. If we assign a number to each current occupant that is twice the room number, then the initial correspondence between rooms and occupants is the one shown in Correspondence 9 above, with A representing the rooms and B the occupants. If each occupant moves to a room whose number is equal to the current room number plus 6, then the correspondence between rooms and occupants is the one shown in Correspondence 11 above, which frees up 6 rooms. By physically changing the relationship of occupants to rooms, we change the correspondence expressed by that relationship. And by changing the expressed correspondence, we change whether there are unpaired rooms, or unpaired occupants. If we were to change the expressed correspondence to Correspondence 7 above, it would free up infinitely many rooms, namely all the rooms with odd numbers. If we were to change the expressed correspondence to Correspondence 10 above, it would put 3 occupants in every room without freeing up any rooms.
67. Of course, occupants must actually change rooms. It wouldn’t do any good to just change the numbers on the rooms, for example. That would change the expressed correspondence between rooms and numbers, but not between rooms and occupants. Also, Guminski’s proposal to add more rooms to the hotel, while unnecessary, would certainly work. But if more rooms are added, the hotel will have compositionally more rooms, but not numerically more rooms. Also, if all room numbers are to be natural numbers, the room numbers assigned to these added rooms would have to be the same as numbers currently assigned to existing rooms. If the room numbers must be unique, then the numbers of infinitely many existing rooms would have to be changed to free up numbers for the added rooms. Thus we would still end up having infinitely many occupants in rooms with different numbers.
68. In addition, infinitely many people must change rooms more or less simultaneously if we assume that each room must be vacated before the next occupant moves in. This does not mean the process will necessarily finish in a finite amount of time, although it could. If a finite subset of occupants were to be the first to move, they could only swap rooms with each other, since there would be no other vacant rooms to move to. But this would not free up any rooms, so there would be no point in making them move. Only moving an infinite number of occupants would free up any rooms. But it’s not necessary to move everyone. Moving any infinite subset of occupants will do. For example, if just the people in rooms where the room number ends with the digits 7539376939205 were to move, it would still be possible to free up any number (including an infinite number) of rooms.
Inches and Feet
69. Guminski says “there cannot be a one-to-one correspondence between an infinite set of feet and an infinite set of inches.” (AG1.24) To see why this is not so, imagine a board, the leftmost two feet of which are shown in Figure 2. Imagine this board extends without end on the right. Pegs are fastened to the board at one-inch intervals, numbered consecutively from left to right starting at one. Beside every twelfth peg is a slightly larger peg, and these are also numbered consecutively from left to right starting at one. There is an obvious twelve-to-one correspondence between the smaller pegs and the larger pegs that expresses the conventional correspondence of inches to feet. Now imagine infinitely many strings, each with one end tied to a smaller peg and the other end tied to the larger peg with the same number. (Only the first two strings are shown in the figure to keep it from being too cluttered.) The strings express a one-to-one correspondence between inches and feet. The bijective function m mapping inches to feet is ƒ = m(i) = i. The use of strings to connect corresponding elements may remind you of the robots in Figure 1 since strings are used in both figures to express the one-to-one correspondence.[34]
Figure 2: Correspondence of Inches to Feet:

70. Going from left to right, each string is longer than the previous one. If we say that a string points from the smaller peg to the larger peg, then all the strings point to the right. If the board were cut, the left section would be finite but the right section would still be infinite. If it were cut so that the number of the last small peg on the left section is a multiple of twelve (for example, if it were cut to include just the part shown in the figure above), then the twelve-to-one correspondence of smaller pegs to larger pegs would still apply in both sections. But there is no place where the board could be cut such that a one-to-one correspondence would apply in the left section. Such a correspondence can apply only to an infinite section.
71. Now imagine the board also extends indefinitely to the left as shown in Figure 3. The strings attached to pegs with negative numbers point to the left and get longer the farther you go to the left. Moreover, the board could be cut and a one-to-one correspondence would apply to each section, since both would be infinite.
Figure 3: Positive and Negative Inches and Feet:

Library with Infinitely Many Books
72. Another so-called absurdity, which Guminski cites as one of Craig’s favorites, concerns a library with infinitely many red books and infinitely many black books. (AG1.33) Craig says the one-to-one correspondence of all books to just red books is absurd. But change the following terms and this is just the first example all over again.
- all books ⇒ all hands
- black books ⇒ right hands
- red books ⇒ left hands
73. I cannot help but point out Craig’s blatant appeal to intuition. He asks: “But would we believe someone who told us that the number of red books in the library is the same as the number of red books plus the number of black books?”[35] He expects us to answer no because he assumes it’s intuitively obvious that having compositionally more elements always means having numerically more. But this in turn assumes that, in the absence of experience, intuition is a better guide to reality than the rigorous logic of mathematics.
Absurdities Involving Time
Years Up Through a Particular Year
74. Another supposed absurdity involves the “(hypothetical) infinite set of years ending in the year 1000 and that set ending in the year 2014.” (AG1.35) Both Craig and Guminski appear unable to discern the following obvious (or so I would have thought) one-to-one correspondence between these two sets:
Function: a = ƒ(b) = b + 1014
Inverse: b = g(a) = a – 1014
A: ... 2010 2011 2012 2013 2014 B: ... 996 997 998 999 1000
75. My guess is they ignored this correspondence because they assumed that each year must correspond with itself. Such a requirement would indeed make a one-to-one correspondence impossible. But of course, there is no such requirement.[36] Closely related to this is Craig’s belief, quoted in AG2.26, that if the past is infinite, then “the number of events that have occurred up to the present is no greater than the number that have occurred at any point in the past” and this is inconsistent with the obvious fact that new events are occurring all the time. Here Craig is committing two errors. First, he mistakenly assumes that a one-to-one correspondence between infinite sets precludes any other correspondence. And second, he again fails to distinguish between having numerically more and compositionally more elements.
76. In the previous example, time is only incidentally an issue. But in the case of Tristram Shandy (AG1.36), it’s a very significant part of the problem. To my knowledge, the first person to discuss this was Bertrand Russell, who wrote:
Tristram Shandy, as we know, employed two years in chronicling the first two days of his life, and lamented that, at that rate, material would accumulate faster than he could deal with it, so that, as years went by, he would be farther and farther from the end of his history. Now I maintain that, if he had lived for ever, and had not wearied of his task, then, even if his life had continued as eventfully as it began, no part of his biography would have remained unwritten. For consider: the hundredth day will be described in the hundredth year, the thousandth in the thousandth year, and so on. Whatever day we may choose as so far on that he cannot hope to reach it, that day will be described in the corresponding year. Thus any day that may be mentioned will be written up sooner or later, and therefore no part of the biography will remain permanently unwritten. This paradoxical but perfectly true proposition depends upon the fact that the number of days in all time is no greater than the number of years.[37]
77. Perhaps the best way to look at this is to compare it to the correspondence of inches and feet discussed above. To apply this to Tristram Shandy, make the following changes:
- inches ⇒ days
- feet ⇒ years
- 12-to-one ⇒ 365-to-one
78. The main difference between these two examples is that there is no such thing as a physical string that can tie together two different points in time. But the one-to-one correspondence is not a physical connection, but rather the bijective function mapping days to years, namely y = m(d) = d.[38] However, there is one other very important difference, which is that since the pegs now represent points in time, it’s unclear in what sense those pegs representing future time exist. One interpretation is that only the pegs up through the present exist, and each day a new smaller peg is added, and each year a new larger peg. The present thus represents a point at which the board is cut, though it’s a point that’s constantly moving to the right.
79. When Bertrand Russell granted Tristram Shandy immortality in the passage quoted above, he unfortunately used the pluperfect subjunctive, saying “if he had lived for ever … no part of his biography would have remained unwritten.” The subjunctive mood is appropriate, of course, since this is a counterfactual hypothetical. But the pluperfect (“if he had lived” instead of “if he were to live”) is misleading. The pluperfect implies a point that is in the past relative to some other point in time. This phrasing implies there is (or will be) a time when Tristram Shandy’s life is complete and every part of his autobiography has been written. But of course there is no such time. No matter where we are in the timeline, there is more to go. To think otherwise would be to fail to grasp the meaning of forever.
80. Regarding this supposed absurdity, Guminski makes an important—and valid—point: “At the end of any given year Tristram Shandy will at best have written about only one of the 365 days of the same year thereby always keeping hopelessly behind with his autobiography.” (AG1.36) Although the timeline goes on forever, there is no point in time when the one-to-one correspondence holds. This brings us back to the question I first raised about Ty when he was attaching strings to the robots’ hands: Can he finish the task in an infinite amount of time, or will he never be able to finish it? Similarly, can Tristram Shandy finish his autobiography in an infinite amount of time, or will he never finish it? The answer is clearly that he can never finish it, since finishing it would mean his life has ended, which contradicts the assumption that he will live forever.
81. Now you may justly wonder how I can maintain that there is a one-to-one correspondence of days to years when there is no point in all of eternity when this correspondence is expressed. The correspondence exists because there is no day in Tristram Shandy’s eternal life that he will not eventually write about. If time is eternal, its infinitude cannot itself exist in time any more than אo can be an element of ℕ. Its infinitude can only be viewed the way Boethius supposes that God views it[39], or to use Spinoza’s apt phrase, sub specie æternitatis (under the aspect of eternity). Or to return to the correspondence of inches and feet, any point in time corresponds to a place where the board is cut. But a one-to-one correspondence cannot hold over any finite segment of the board. Similarly, it cannot hold over any finite segment of time.
82. If we suppose Tristram Shandy’s life is eternal not just in the future, but also the past, and therefore he has already spent an infinite amount of time writing, this would still not mean he can complete his autobiography. To see why, consider Figure 3 if it’s adjusted from inches-and-feet to days-and-years. The fact that the strings point to the left when the numbers are negative means that Tristram Shandy is writing about events before they occur. And the farther to the left—that is, the farther back in time—the farther ahead Tristram is in his writing. What cannot be the case is for Tristram to have been writing for an infinite amount of time while always writing about days that he lived prior to writing about them.[40]
The Central Issue
83. The common thread that appears to be the reason that both Craig and Guminski believe these are counterintuitive absurdities (in SV) is the assumption that a correspondence between two real sets must be a physical connection between corresponding elements rather than a function—an algorithm or rule—specifying which items correspond. Set theory says there is a one-to-one correspondence between any two sets with the same cardinality, and Craig and Guminski point to cases where that correspondence is not expressed as examples of counterintuitive absurdities. Craig doesn’t seem to be aware that any other correspondence is possible. Guminski more perspicaciously realizes that some other correspondence is expressed and has devised AV to explain why the one-to-one correspondence does not exist. But of course, it does exist. It just isn’t expressed.
84. Central to AV is the thesis that “Unlike mathematical infinites, whether or not two real infinites are equipollent to each other depends upon the existence of a factually contingent or definitional matter pertaining to real entities.” (AG1.24) But it’s not the equipollence itself that is dependent on this matter, but only whether that equipollence is expressed. Indeed, of all the infinitely many correspondences that exist between two real infinites, it would be unusual for more than one to be expressed. Once that is realized, it becomes clear that the counterintuitive absurdities are not absurdities at all.
85. It would not be unreasonable for Guminski to reply that when I say correspondences exist even when they’re not expressed, this isn’t real existence, but only some kind of abstract mathematical existence. Even if that’s true, there is clearly no expectation for every possible correspondence between two real sets (whether finite or infinite) to really exist in the sense of being expressed. So when applying Cantorian theory to the real world (using SV), what reason is there to think a one-to-one correspondence must exist in this sense when there is no such requirement for any other correspondence?
Infinite Temporal Series
86. I find myself in almost complete agreement with Guminski’s second paper (AG2), where he rebuts Craig’s second argument that an infinite temporal series is impossible even if it’s possible for a real infinite to exist. In fact, I find only two things in it to criticize. First, Guminski invokes AV in several places to counter certain arguments that he believes exploit deficiencies in SV, when the problem is not in SV, but in the way it’s been misunderstood. And second, I think he should have gone further and declared Craig’s argument to be circular.
87. Illustrating my first criticism, in AG2.29-40 there is a discussion of whether it’s possible for a counter to count down through the years of a beginningless past. Craig makes two arguments against this, both based on the “principle of correspondence” in Cantorian theory. For his first argument Guminski quotes him as saying “the counter should at any point in the past have already finished counting [down] all the numbers, since a one-to-one correspondence exists between the years of the past and the negative numbers.” (AG2.38)[41] Craig’s second argument is that if a second counter is counting down through days instead of years, both counters would finish at the same time despite counting at different rates. Both these arguments are obviously based on Craig’s faulty understanding of the principle of correspondence.[42]
88. Guminski blames both of Craig’s errors on SV. (AG2.39) He correctly points out that the two counters—one counting down days and the other counting down years—have a 365-to-one correspondence. Thus they will have the same count only on the day they reach zero and the day before. But of course, this does not contradict SV, which asserts that the two counters have this and infinitely many other correspondences. The fact that the 365-to-one correspondence is the only one that is expressed is entirely consistent with SV, while Craig’s errors are not.
89. Before proceeding to my second criticism, it will be helpful to first identify the following two relevant general principles:
| Principle | Definition |
|---|---|
| Finite closure | When a finite set of new elements is added to an existing finite set[43], the resultant set is also finite. Moreover, there is no limit to how many times this can be done. |
| Instantaneous transition | As a corollary to the principle of finite closure, the only way to transition from a finite set to an infinite set is to add infinitely many new elements in a single operation. |
90. In addition, consider the following statements:[44]
- The universe has a beginning.
- There was a first event in time.
- Past time is finite.
- The universe was created.
91. The first three statements are equivalent. The fourth implies the other three but is not implied by them unless we can exclude the possibility that the universe came into existence uncaused. Since the first premise of KCA is “Everything that begins to exist has a cause of its existence”[45], and we’re discussing whether Craig’s argument is circular, we can make this exclusion, thereby making all four statements equivalent. Consequently, proving any one proves them all. By the same token, assuming any one in order to prove any of the others would be begging the question.
92. Craig’s second argument is based on the premise that “a temporal series of events is a collection formed by successive addition and that a collection formed by successive addition cannot be an actual infinite.” (AG2.13) He explains: “The reason is that for every element one adds, one can always add one more. Therefore, one can never arrive at infinity. What one constructs is a potential infinite only, an indefinite collection that grows and grows as each element is added.” (AG2.15)[46] Now if Craig is simply stating the principle of finite closure, then like Guminski, “I readily agree that Craig is quite right when he asserts that a collection formed by successive addition cannot be an actual infinite.” (AG2.17) Yet I can’t help thinking Craig is arguing that even if time flows from one moment to the next without end, somehow this means it’s not eternal.
93. The phrase potential infinite always refers to something that can increase without limit while remaining finite. But this is possible only because it’s a sequence of elements from an infinite set. The natural numbers can be counted forever without arriving at infinity, but it would be a mistake to say N is only potentially infinite. Infinity is not a destination to be reached, but rather a journey that never ends. Far from showing that it’s not infinite, the fact that the destination can never be reached is precisely what makes it infinite. If future time is eternal, it’s not because a point is reached where an infinite amount of time has elapsed since some arbitrary starting point. It’s because time never ends, which means time as a whole (which includes all future time) is infinite, even though the elapsed time is always finite.[47]
94. Guminski masterfully shows that Craig has fallaciously assumed that because every finite segment of time is formed by successive addition, this must be true of time as a whole. (AG2.18-21) Guminski rightly calls this “an instance of the fallacy of division.” (AG2.20) But this conclusion does not depend on AV. It also leads to my second criticism of AG2, namely that Guminski never clearly states that Craig’s argument begs the question. He does point out that when Craig speaks of a “collection [as] having been successively formed he is always referring to the case of one that must have a first member.” (AG2.15) Indeed, if Craig’s argument is based on the principle of finite closure, then he must be assuming that the set of temporal events was at one time finite. (Cf. AG2.17) But this is the very thing he’s trying to prove.
95. Craig presents two variations of his argument that Guminski does not address. Since they differ significantly from the main form of the argument, a separate response is appropriate. One is a version Craig borrows from G. J. Whitrow:
[I]f the chain of events prior to [the event] E is infinite, then there must be an event O that is separated from E by an infinite number of intermediate events. If not, then the number of events separating E from any event O would be finite, and thus the past would be only a potential infinite, which is impossible.[48]
96. This specious argument shows a failure to grasp that an infinite set can consist entirely of finite elements. The argument says, in effect, that if there are infinitely many negative integers less than (say) -1, then there must be a negative integer n such that there are infinitely many integers between n and -1, since otherwise the total number of negative integers would be finite. Such an argument would be inexcusable in an undergraduate mathematics class. Even though there are infinitely many negative integers, every one of them is finite, as is the number of integers between any two arbitrarily selected negative integers.
97. The other variation of Craig’s argument asserts that a real infinite can exist only by being instantaneously created:
For if the series or collection of events is always infinite, it cannot have been formed by successive addition. It would be just given at some point, which is absurd, being contrary to the nature of time. For though God could create the universe ex nihilo with the appearance of age, even He could not create the world ex nihilo actually having a past, to say nothing of an infinite past. But this is the only way a series of events could be formed, if it is to be always actually infinite. If it is formed by successive addition, it will have to be a potential infinite.[49]
98. Far be it from me to dispute the limits of omnipotence, but if it’s agreed that it excludes the ability to do something self-contradictory, then Craig is correct that God could not create the world with an infinite past. Implicit in the concept of creation is the notion that the created thing begins to exist at the moment of its creation. Consequently, a beginningless universe could not have been created. But which question is Craig begging here? On the one hand, he’s trying to prove the universe requires a creator, so it would be circular to argue “The universe must have a beginning since otherwise God couldn’t have created it.” On the other hand, his argument is based on the principle of instantaneous transition. But this can be applied to the past only if there is a transition, that is, only if it’s already known that at one time the past was finite, which again is the very thing to be proved. Or is it possible Craig is simply oblivious to the fact that he is using the word formed as a synonym for created, thereby implying a moment of creation? Yet again, this assumes the thing to be proved.
Conclusion
99. Arnold T. Guminski’s alternative version of the application of Cantorian theory to the real world attempts to solve the problem of counterintuitive absurdities he believes result when applying Cantorian theory to the real world using what he calls the standard version. I find myself unable to accept AV because of three serious problems:
- AV is a set of a priori rules purporting to tell how to apply a system of pure mathematics—namely Cantorian set theory—to the real world. But what’s needed is a model and a posteriori confirmation, that is, empirical evidence. The model identifies what in the real world the math applies to and the empirical data tells whether the math applies. The use of a priori rules is no more than intellectual speculation that doesn’t take us out of the realm of pure mathematics.
- AV doesn’t actually tell how to apply Cantorian theory to the real world. Instead AV tells how to change it in order to apply it. Moreover, AV changes it in ways that make it inconsistent. If these changes are truly necessary, then it shows that Cantorian theory doesn’t really apply to the real world and a non-Cantorian set theory is needed. Unfortunately, there currently is no such thing as a non-Cantorian set theory, and without actually developing such a theory, there is no way to know if there can be one that is compatible with AV.
- AV is unnecessary because there is no reason to suppose that counterintuitive absurdities would result from applying Cantorian theory to the real world. The arguments claiming there are such absurdities are based on a misunderstanding of the mathematics of infinite sets. In particular, the arguments depend on two erroneous assumptions, namely (1) that a one-to-one correspondence between real infinite sets must be expressed, when all that’s really required is a rule specifying which elements correspond, and (2) that a one-to-one correspondence is inconsistent with the correspondence that’s actually expressed. Since Craig’s first argument against a beginningless universe is based on these alleged counterintuitive absurdities, their nonexistence is sufficient to refute it.
100. On the other hand, Guminski’s rebuttal of Craig’s second argument is perfectly sound. Craig has argued as if infinite sets must have the same properties as finite sets. Specifically, because a finite sequence of temporal events must include a first event, he seems to think an infinite sequence must as well. Guminski has ably shown this is a fallacy. However, Guminski’s argument here does not depend on AV, and it stops short before declaring that Craig’s argument is circular.
Notes
[1] When referring to Guminski’s two articles I will use AG1 to refer to “The Kalam Cosmological Argument: The Question of the Metaphysical Possibility of an Infinite Set of Real Entities” and AG2 to refer to “The Kalam Cosmological Argument Yet Again: The Question of the Metaphysical Possibility of an Infinite Temporal Series.” When either of these symbols is followed by a dot and a number, the number is a paragraph number, unless preceded by the letter F, in which case it’s a footnote. Also, whenever any part of quoted text is in italics, the italics are in the original, regardless of the source, unless otherwise noted.
[2] The symbol ℕ (the letter N in blackboard bold) is the standard symbol for the natural numbers, which are the counting numbers 1, 2, 3, and so on. Sometimes 0 is also included in the natural numbers.
[3] Neither am I a mathematician, although I do have a bachelor’s degree in mathematics.
[4] The basic concepts and features of set theory used in this paper include the following:
- A set is simply a collection of things. The things in the set are called elements or members. There are several ways to identify the elements in a set, including:
- Enumeration: The most common way to notate a small set is to list its elements enclosed in curly braces. For example, Dairy = { Milk, Eggs, Cheese } defines a set named “Dairy” with 3 elements, namely, Milk, Eggs, and Cheese. Generally, the order of the elements is irrelevant, but not always, especially when the elements are numbers.
- Criteria: A set can also be defined by specifying one or more criteria for membership. For example, the elements of a set defined as “all female residents of New York City over the age of 65” meet three criteria, namely being (1) female, (2) a resident of New York City, and (3) over the age of 65.
- Implication: Numerical order can be used to implicitly include elements in a set by using an ellipsis to mean a pattern is repeated. For example, A = { 2, 4, 6, … , 32 } defines a set named A whose elements are the even numbers from 2 through 32. If the ellipsis is the last thing before the closing curly brace, it means the pattern goes on forever. Thus E = { 2, 4, 6, … } defines a set named E whose elements are all the even numbers, without end.
- A set can have no elements, in which case it’s called the empty set or the null set. The symbol ∅ is used for the empty set. Thus ∅ = { }.
- The notation a ∈ X is used to mean a is an element in the set X. By convention in this paper I use uppercase letters to name sets and lowercase italic letters to name elements of a set.
- The concept of subsets and supersets is very important. If S and T are sets and every element in S is also in T, then S is a subset of T. This is notated as S ⊂ T. If S is a subset of T, then T is a superset of S. If T contains other elements that are not in S, then S is said to be a proper subset of T. A set is a subset of itself, but not a proper subset of itself. The empty set is a subset of any set.
- Another very important concept is cardinality. The cardinality of a set is simply the number of elements in the set. For example, the cardinality of the set Dairy defined above is 3. Cardinality is very straightforward when the number of elements is finite, but less so when it’s infinite. To make the concept useful for both finite and infinite sets, we use the idea of one-to-one correspondence to determine whether two sets have the same cardinality. A one-to-one correspondence is defined by a bijective function, which I will explain more fully later in this paper. But the basic idea is that two sets have a one-to-one correspondence if every element of each set can be paired up with exactly one element from the other set. When two sets have a one-to-one correspondence, they are said to be equivalent, equinumerous, equipotent, or equipollent. Guminski prefers the last of these terms (AG1.7), so I will use it as well.
- There are infinitely many natural numbers, so the cardinality of the set of natural numbers cannot itself be a natural number. The number invented to represent this cardinality is אo (the Hebrew letter aleph with the subscript 0, which can be read as aleph-zero, aleph-null, or aleph-naught). Because the natural numbers are used for counting, a set whose cardinality is אo is said to be countable or denumerable. There are also sets that are uncountable whose cardinality is greater than אo. In fact, there are infinitely many cardinal numbers greater than אo, but I will not be dealing with them in this paper.
- There are a number of operations that can be performed on sets, of which the following two are used in this paper. To illustrate them, let P = { 1, 2, 3, 4 } and Q = { 3, 4, 5, 6 }.
- Union: The union (notated by the symbol ∪) of two sets is the set consisting of all elements that are in either set. Thus, P ∪ Q = { 1, 2, 3, 4, 5, 6 }. The common elements, 3 and 4, are included only once in the union because the elements of a set must be distinct. Thus the cardinality of P is 4 and the cardinality of Q is 4, but the cardinality of their union is only 6.
- Intersection: The intersection (notated by the symbol ∩) of two sets is the set consisting of elements that belong to both sets. Thus P ∩ Q = { 3, 4 }. If two sets have no elements in common, then their intersection is the empty set. In that case the two sets are said to be disjoint.
[5] There are only two features of algebra used in this paper. First is the concept of a function. A function is a relation between in input value and an output value. The usual notation for a function is y = ƒ(x) (which is read as “y equals ƒ of x“), where ƒ is the function, x is the input, and y is the output—or rather y is set equal to the output. The choice of letters is arbitrary. A function has the following features:
- A domain, which is the set of allowable input values.
- A codomain (sometimes called the range), which is the set of possible output values.
- An image, which is the set of actual output values.
- A definition, which is typically a formula or algorithm telling how to compute the output from the input. If the function is defined as a formula, the formula is often written after the function declaration. For example, q(m) = 2m+3 would say the function q is defined by the formula 2m+3, so the function value is computed by doubling the input and adding 3.
In this paper I frequently write functions in the form a = f(b) = b + 1 to emphasize that the right side of the equation a = b + 1 is the definition of a function whose input is b, and the left side is a variable whose value is equal to the output of the function. I do this because it’s important to understand that a function is what defines a correspondence.
A function may have an inverse, which is a function that reverses the original function. This leads to the second feature of algebra used in this paper, namely solving an equation for a variable. For example, if the function ƒ is defined as a = ƒ(b) = b + 1, then the inverse function g can be found by solving for the variable b, yielding b = g(a) = a – 1. Thus if the input to ƒ is 5, for example, the output is 6. If 6 is the input to g, the output is 5. Thus g reverses ƒ because it takes you back to the input you started with. This means each function is the inverse of the other.
[6] Immanuel Kant, Critique of Pure Reason from The European Philosophers from Descartes to Nietzsche (New York: Random House, 1960), pp. 381-382.
A statement is said to be synthetic if knowledge of the real world is needed to know whether the statement is true. The opposite would be an analytic statement, whose truth is known simply by understanding the syntax and the meaning of the words. For example, the statement “Edentulous creatures are toothless” is analytic because the word edentulous means toothless. No knowledge of real creatures or teeth is required to know the statement is true. On the other hand, “Anteaters are edentulous” is synthetic because the statement can’t be known to be true without knowledge of actual anteaters. Moreover, there is always the possibility that someone will discover a species of anteater with teeth, thus falsifying the statement. But there is absolutely no chance of someone discovering an edentulous creature with teeth because that would be a contradiction in terms.
In general, the truth of analytic statements can be known a priori, that is, prior to any experience with whatever the statements are about. On the other hand, whatever can be known only a posteriori, that is, only after experiencing it or learning about someone else’s experience with it, is described by synthetic statements. More simply, this boils down to these two statements:
- Analytic implies a priori.
- A posteriori implies synthetic.
And here is the converse of each of the two statements:
- A priori implies analytic.
- Synthetic implies a posteriori.
There is general agreement that the first two statements are true. But whether the last two statements are true has been a matter of much philosophical debate—at least prior to the twentieth century. One of the foundational assumptions of Kant’s philosophy is that the last two statements are false. When Kant says that mathematics is both synthetic and a priori, he’s saying that mathematics gives knowledge of the real world without first requiring actual experience of whatever the math is being applied to.
[7] A brief history of this development can be found in Burnett Meyer, An Introduction to Axiomatic Systems (Boston: Prindle, Weber & Schmidt, Incorporated, 1974, pp. 3-8). For a thorough treatment as part of a more complete history of mathematics, see Morris Kline, Mathematics: The Loss of Certainty (New York: Oxford University Press, 1980).
[8] Ernest Nagel and James R. Newman, Gödel’s Proof (New York: New York University Press, 1958, pp. 45-46).
[9] Ernest Nagel and James R. Newman, Gödel’s Proof, p. 12.
[10] Bertrand Russell, Mysticism and Logic (New York: Double Day Anchor Books, 1917), p. 71.
[11] In the propositional calculus, variables are usually represented by lowercase letters, and connectives by special symbols. In the standard model, a variable is a proposition, which has a truth value, that is, it’s either true or false. Propositions and connectives are combined into formulas, which also have truth values. The following table shows two such connectives, formulas using those connectives, and what the formulas mean.
| Connective | Circuit | Formula | Meaning | Equivalent Meaning |
|---|---|---|---|---|
| ∧ (and) | Series | p ∧ q | p and q are both true. | The formula is true if and only if the individual propositions are both true. |
| ∨ (inclusive or) | Parallel | p ∨ q | Either p or q or both are true. | The formula is false if and only if the individual propositions are both false. |
To understand the Circuit column in the table, consider a simple electrical circuit consisting of a power source, two switches, and a light. The switches and light each have two states, namely on and off, which correspond to true and false, respectively. The switches are the variables, corresponding to propositions, and the light corresponds to the formula. If the switches are wired in series, then the light will be on if and only if both switches are on. If the switches are wired in parallel, then the light will be off if and only if both switches are off. In this model, the circuit itself is the connective.
Similarly, a logic gate on a computer chip is an electronic model for the propositional calculus where the logic gate is the connective, its inputs are the variables, and its output is the formula. Technically, logic gates implement Boolean algebra rather than the propositional calculus. But the two systems are similar enough to be interchangeable for the purposes of this discussion, and the propositional calculus is more intuitively accessible to the nonmathematician. Moreover, to the extent that the two systems are interchangeable, they can be viewed as two models of the same system.
[12] Albert Einstein, Relativity (New York: Crown Publishers, 1961), pp. 113-114.
[13] Bertrand Russell, A History of Western Philosophy (New York: Simon and Schuster, 1945), p. 716.
[14] Arithmetic was codified as an axiomatic system by Giuseppe Peano (Morris Kline, Mathematics, pp. 189-192), and as such is part of pure mathematics.
[15] Burnett Meyer, An Introduction to Axiomatic Systems, p. 8.
[16] This is obviously a very broad topic that extends far beyond the scope of this essay, so I will mount only a very brief defense of my position. The axioms in any branch of pure mathematics are (up to a point) arbitrary. But when an attempt is made to apply mathematics to the real world, then the question of whether the axioms are true in the real world becomes very important. It’s generally sufficient for the axioms to be approximately true, but if any are clearly false, the entire system becomes useless. The initial assumptions in inductive inferences are also arbitrary, up to a point. The difference is that these assumptions are repeatedly tested (when induction is viewed as a process), and modified when they don’t pass the test. Thus with induction it’s possible to end up with the truth even when starting from a false assumption. The idea that induction must assume the uniformity of nature as some sort of axiom simply misconstrues how induction works. The uniformity of nature is being tested with virtually every inductive inference, and being more strongly confirmed each time. This is not circular reasoning, because if nature were not uniform, the assumption of uniformity would fail the tests. Of course, there can be no such thing as the final truth, because we can never be sure that more testing won’t force us to alter the current inductive inference. Moreover, since most of our reasoning is a combination of induction and deduction, it’s subject to errors of both types of reasoning. Thus it would be a mistake to assume that an argument that is partly inductive is safe from circular reasoning.
When I speak of viewing induction as a process, I mean that we rarely make a single inductive inference about something. As we have new experiences, we constantly compare them to expectations that we have developed inductively. As a result, our expectations are either reinforced or reevaluated. But each such experience is a new instance of a previous inductive inference. And all these instances constitute a process. Such a process is vaguely similar to the scientific method, though far less rigorous and far more prone to error.
[17] In fact, I would say it means less. I would argue that the only way we can know whether or to what degree deductive logic applies to the real world is inductively. Since inductive knowledge is never certain, the certainty that normally accompanies deductive logic is lost when it’s applied to the real world. Obviously this makes it very hard to maintain that anything is metaphysically necessary, that is, that there’s anything in the real world that must be the case.
[18] Guminski defines what he means by the term Cantorian in AG1.F10:
I use “Cantorian theory” in a broad sense to include naïve set theory or any axiomatic set theory (such as that of Zermelo–Fraenkel set theory) in pure mathematics that accepts the notion of an actual mathematical infinite and includes the propositions that one-to-one correspondence between sets is the necessary and sufficient condition of the sets having the same cardinality, and that every such infinite set has at least one proper subset with which it is in one-to-one correspondence.
Although AV accepts the notion of an actual mathematical infinite, it explicitly denies the other two propositions Guminski mentions. This would seem to make it prima facie non-Cantorian. But because he says AV is a set of bridging rules, and these are not part of the set theory itself, I don’t believe he thinks of AV as being non-Cantorian.
[19] I use the term non-Cantorian to mean any axiomatic set theory in which at least one axiom is inconsistent with the axioms of the set theories that Guminski describes as Cantorian. The axioms of Zermelo–Fraenkel set theory, for example, are written in the language of first order logic, which in turn is an extension of the propositional calculus. Thus a non-Cantorian set theory would have at least one axiom that contradicts at least one axiom in Zermelo–Fraenkel set theory, or first order logic, or the propositional calculus.
[20] In the analogy I’m about to make, Goofian arithmetic corresponds to Cantorian theory because neither accurately describes reality, although this failure is only hypothetical in the case of Cantorian theory.
[21] In AG1.F16, Guminski indicates he does not believe this is what it means to have the same cardinality, although he admits that “Cantor and others understood” it that way. In fact, Cantor wrote “Of fundamental importance is the theorem that two aggregates M and N have the same cardinal number, if and only if, they are equivalent.” (Georg Cantor, Contributions to the Founding of the Theory of Transfinite Numbers, Dover Publications, Inc., New York, 1955, p. 87, emphasis added) Although Cantor calls it a theorem, in modern set theory equivalence (equipollence) and equal cardinality are both defined by a bijection.
[22] The following arrangement shows the beginning of a one-to-one correspondence between an infinite set A and ℕ, and also between ℕ and another infinite set B. Clearly an corresponds to bn for every natural number n.
| A | ℕ | B | ||
|---|---|---|---|---|
| a1 | ↔ | 1 | ↔ | b1 |
| a2 | ↔ | 2 | ↔ | b2 |
| a3 | ↔ | 3 | ↔ | b3 |
| … |
The proof that equipollence is transitive belongs to pure mathematics, and although the above arrangement makes it intuitively obvious that it also applies to real sets, the lack of empirical evidence for infinite sets ought to temper our confidence in that conclusion. Nonetheless, I can’t think of a way to redefine a one-to-one correspondence so that it’s not transitive for infinite sets, nor does Guminski tell us how. And with neither a definition nor empirical data to support it, I see no reason to accept the idea.
[23] These criteria can also be stated as follows:
- u(b) ∈ C for all b ∈ B, that is, every element of B maps to an element of C.
- u(i) ≠ u(j) when i ∈ B, j ∈ B, and i ≠ j, that is, no two distinct elements of B map to the same element of the codomain.
- v(c) ∈ B for all c ∈ C, that is, every element of C maps to an element of B.
- v(i) ≠ v(j) when i ∈ C, j ∈ C, and i ≠ j, that is, no two distinct elements of C map to the same element of the codomain.
A function such as u that that meets the first two criteria (or which meets the
last two, such as v) is called an injective function. The function u
is also surjective if for every c ∈ C, there is an element b ∈ B
such that u(b) = c. It can be shown that if an injective function has an injective
inverse, which is the case if one of the functions meets the first two criteria and
the other meets the last two, then both functions are also surjective. A bijective
function is one that is both (hence the prefix bi) injective and surjective.
Every bijective function has a bijective inverse.
[24] Guminski hints at something vaguely similar in AG1.26 when he talks about an equipollence between the pairs of members of one set and the single members of another set.
[25] A somewhat more formal definition is that a partition of a set X is a set of subsets of X such that (1) the subsets are disjoint and (2) the union of all the subsets in the partition is X. The first criterion ensures that no element is in more than one subset and the second ensures that every element is in at least one subset.
[26] Whether 0 is included in the natural numbers is to some extent arbitrary. I have chosen to exclude it in this paper as a convenience. Also, although the symbol ℕ is the standard symbol for the natural numbers, I have used A in this example just for consistency with the idea of expanding the three sets A, B, and C from finite sets to infinite sets.
[27] When B and C were finite sets, we could check if the function is bijective by inspection, that is, we could look at each element, since there were only 6 in each set, to be sure the function met the criteria for a bijection for each element. Obviously that’s not feasible when the sets are infinite. But proving it for infinite sets is actually no harder than for finite sets.
To prove that c = u(b) = b – 1 is bijective, we need to show that it meets the first two criteria and its inverse b = v(c) = c + 1 meets the other two.
- Every element of B is paired with an element of C.
This amounts to saying that if the input to u is an even number, then the output is an odd number. Since the output is one less than the input, it will always be odd when the input is even.
- No element of C is paired with more than one element of B.
This amounts to saying that if there are two different inputs to u, there will always be two different outputs. It should be obvious that if you have two different numbers and subtract one from each of them, the resulting numbers are also different from each other.
- Every element of C is paired with an element of B.
In other words, if the input to v is an odd number, then the output is an even number. Since the output is one more than the input, it will always be even when the input is odd.
- No element of B is paired with more than one element of C.
In other words, if there are two different inputs to v, there will always be two different outputs. It should be obvious that if you have two different numbers and add one to each of them, the resulting numbers are also different from each other.
[28] B can be partitioned into these 3 subsets:
S1 = { 2, 8, 14, 20, ... }
S2 = { 4, 10, 16, 22, ... }
S3 = { 6, 12, 18, 24, ... }
Each of these subsets has a one-to-one correspondence with A defined by the following bijective functions from which the reader can easily derive the inverses:
Function (S1): s1 = ƒ(a) = 6a - 4 Function (S2): s2 = g(a) = 6a - 2 Function (S3): s3 = h(a) = 6a
[29] To show this, suppose Y is an infinite proper subset of X. Let p be the number of elements of Y that do not correspond to themselves, and assume p is finite. Let q be the number of elements of X that are not in Y. Now q could be finite or it could be infinite, but it can’t be 0. Certainly these q elements cannot correspond to themselves, since they don’t exist in Y. Now there are p elements in Y that do not correspond with themselves, and p + q elements in X that do not correspond with themselves. So the p elements in Y must correspond with the p + q elements in X, but that cannot be a one-to-one correspondence since p is finite and q > 0. Thus there cannot be a one-to-one correspondence between a set and one of its proper subsets where all but a finite number of elements correspond with themselves.
[30] To be clear, it’s not the inexhaustibility of the supply of robots and hands that ensures there is a one-to-one correspondence. If one set were a countable infinite but the other were an uncountable infinite, both would be inexhaustible, but there could not be a one-to-one correspondence between them. It’s only the existence of a bijective function that ensures a one-to-one correspondence.
In this case, we’re dealing with 4 sets, namely the set R of robots, the set H of hands, the set D of right hands, and the set S of left hands. (Because robots and right both begin with the letter R, I’ve chosen to use D for dexter and S for sinister, the Latin words for right and left, respectively.) Now D ∪ S = H (that is, every hand is either a right hand or a left hand), while D ∩ S = ∅ (that is, no hand is both a right hand and a left hand), so D and S constitute a partition of H. Now initially the expressed correspondence of robots to hands is this:
Bijective function mapping R (robots) to D (right hands): d = g(r) = 2r – 1
Bijective function mapping R (robots) to S (left hands): s = f(r) = 2r
H: 1 2 3 4 5 6 7 8 ... / / / / R: 1 2 3 4 ...
The backslashes () in the middle row are the robots’ right arms (I’m assuming the robots are facing us, so their right is our left) and the slashes (/) are their left arms. Thus the odd numbered hands are right hands and the even numbered hands are left hands. Since D and S form a partition of H, and they each have a bijective function mapping them to R, there is a two-to-one correspondence of H to R, exactly as Guminski claims. Now after removing and reattaching the hands, the expressed correspondence of robots to hands is this:
Bijective function mapping R (robots) to H (all hands): h = f(r) = r
H: 1 2 3 4 ... / / / / R: 1 2 3 4 ...
The bijective function means there is a one-to-one correspondence between robots and all hands, contrary to what Guminski claims. The only thing that’s changed is the physical arrangement of robots and hands, and thus the correspondence that’s expressed by that arrangement. But all the correspondences are there all along, whether they’re expressed or not. To be sure, Guminski is right when he points out that, prior to removing their hands, the one-to-one correspondence maps every robot except the first to a hand on a different robot. This amounts to saying the one-to-one correspondence is not expressed by the physical arrangement.
[31] Suppose Ty works at a consistent pace with no breaks, and it takes him t seconds to attach the strings to each robot, then the time when he finishes attaching the strings to robot n will be n × t seconds after he begins his task. This is a finite number no matter what the value of n because the number assigned to every robot is finite. Thus every robot will have its strings attached within a finite time from when Ty begins his task. But the total number of robots is אo, so the total amount of time Ty will spend on the task is אo × t seconds, which is infinite. If this seems like a contradiction, recall that every natural number is finite, but the total number of natural numbers (which is the cardinality of ℕ) is אo. It will be very important to remember this distinction when we reach the section on infinite temporal series.
[32] As far as I can tell, Hilbert’s Hotel first appears in George Gamow’s book, One Two Three … Infinity (New York: Mentor Books, 1947, p. 28). Gamow attributes the story to David Hilbert and in a footnote declares it to be “From the unpublished, and even never written, but widely circulating volume: ‘The Complete Collection of Hilbert Stories’ by R. Courant.”
[33] William Lane Craig, The Kalām Cosmological Argument (Eugene, Oregon: Wipf and Stock Publishers, 1979), pp. 83-84.
[34] If connecting corresponding elements with strings is not sufficiently persuasive, imagine A and B are two infinite sets of 12-inch rulers, with the natural numbers assigned to the rulers in each set. Thus A and B have a one-to-one correspondence. This correspondence can be expressed by laying the rulers in each set end to end, as shown in Arrangement 1 in Figure 4. Now if the rulers in B are instead laid side by side, as in Arrangement 2, this does not cause the one-to-one correspondence to cease to exist. Yet the arrangement now expresses a one-to-one correspondence between the rulers in B and the inches on the rulers in A. This means B has a twelve-to-one correspondence with A in addition to—and not instead of—these other correspondences.
Figure 4: Correspondence of Rulers:

If this is still not persuasive enough, let n be any natural number, and let S and L be sets of n tiles each, with the tiles in each set laid out in a row. S contains small tiles that are each one inch square, while L contains large tiles that are each one foot square. The following statements are true for any natural number n:
- The length of the row of small tiles is n inches.
- The length of the row of large tiles is n feet.
- The length of the row of large tiles is twelve times the length of the row of small tiles.
- There is a one-to-one correspondence between small tiles and large tiles, that is, between S and L.
- There is a one-to-one correspondence between the inches in the row of small tiles and the feet in the row of large tiles.
Now suppose both sets are infinite, so n = אo. The above statements remain true because each tile still corresponds to a natural number. But there are two important differences. First, each set has an nth tile when n is finite, but not when it’s infinite. And second, because 12 × אo = אo, statement 3 remains true, yet both rows are the same length when the sets are infinite. This should not be surprising, since both rows go on without end. This could be illustrated in Figure 2 by changing the pegs to tiles.
[35] William Lane Craig, The Kalām Cosmological Argument, p. 83.
[36] To be clear, the only requirement for a one-to-one correspondence is a bijection to define it. In this particular case, the bijective function is slightly complicated by the fact that there is no year 0, and years Before the Common Era (BCE) are not written as negative numbers. To compensate, it must be understood that whenever any year y (whether it’s a or b) is nonpositive, it translates to the year (1 – y) BCE.
In the following correspondence, each year does correspond to itself, but the function is not bijective.
Function: a = p(b) = b
Inverse: b = q(a) = a
A: ... 997 998 999 1000 1001 1002 ... 2014 B: ... 997 998 999 1000
I suspect Guminski would argue, in accordance with AG1.26, that without the years 1001 through 2014, we would have A = B, and thus the two sets would be equipollent. So adding those years to A means they are no longer equipollent. As with Hilbert’s hotel, this is half right. Without the years 1001 through 2014 in A, the function p is bijective and ƒ is not. But with those years, p ceases to be bijective, but ƒ becomes bijective.
[37] Bertrand Russell, Mysticism and Logic, pp. 85-86.
[38] What the function y = m(d) = d means depends on where 0 is in the scale of days and years. For the sake of simplicity I have assumed that y = 0 at the moment he begins writing and d = 0 at the start of the first day he writes about. Unless the first day covered in his autobiography is the same day he begins writing, these are different points in time. Those familiar with the Laurence Sterne novels know that Tristram Shandy begins his autobiography with events prior to his birth. In fact, he doesn’t get around to his birth until Volume 3. So to use a common origin for both days and years would require a more complex equation, especially if a more accurate reflection of the novels is desired. However, this would have no effect on the issues discussed in this paper.
[39] Anicius Manlius Severinus Boethius (c. 480-524 AD) was a Roman senator and consul. While imprisoned by the Ostrogothic king Theodoric the Great and awaiting execution, he wrote The Consolation of Philosophy. Among the topics in this work is his solution to the problem of reconciling God’s omniscience with free will, since God’s foreknowledge of the future means that the future is predestined. Boethius argues that God exists outside of time, and sees every event at every point in time all at once. Thus his knowledge of the future is not foreknowledge. In other words, God knows what’s going to happen, but not before it happens, since that would imply God exists in time. (Boethius, The Consolation of Philosophy, New York: Penguin Books, 1969, pp. 150-161.) Guminski cites a similar idea from St. Thomas Aquinas in AG2.F55.
[40] When I say this cannot be the case, I mean that it’s inconsistent with any generally held concept of time. The gap in time between a day that Tristram Shandy lives and when he writes about that day is either finite or infinite. Since there is no point at which it could transition from finite to infinite or vice versa, it must always be one or the other. If it’s finite, then, since it’s constantly increasing going forward in time, it’s decreasing going backward in time and must eventually become negative. When the gap is negative, it means he’s writing about a day that hasn’t happened yet. On the other hand, if today he is writing about a day that is infinitely distant in the past, then he will spend eternity writing about days that are infinitely distant in the past and never get around to writing about today. In this scenario, there are in essence two (or more) timelines. The autobiography describes the days in the first timeline, but is written entirely in the second timeline. Both timelines are endless, but somehow the first is in the past relative to the second.
I should point out that while this second scenario is not consistent with any generally held concept of time, it is consistent with the mathematics of infinite ordinals, although that topic is beyond the scope of this essay. Craig, however, does briefly discuss infinite ordinals (William Lane Craig, The Kalām Cosmological Argument, pp. 75-76). As far as I can tell his purpose is to impress his readers with how counterintuitive they are, since the discussion does not otherwise advance his argument. But since our intuitions about numbers are based exclusively on finite numbers, all he does is show that infinite ordinals are very different from finite ordinals.
[41] The counter is assumed to be counting through the negative numbers and ending with zero, so Craig should have said nonpositive rather than negative. Also, I did not add the word “[down]” in square brackets, but merely copied it from Guminski’s paper. Since the numbers are negative, the counter is actually counting up, not down, which would become obvious if, instead of stopping at zero, it were to continue into the positive numbers. Nonetheless, it’s perfectly reasonable to call this a countdown, since it’s similar to a missile launch, where the time prior to ignition is given as a negative number.
[42] Craig’s first argument is essentially the same as the one concerning the infinite set of years ending in the year 1000 and the set ending in the year 2014. He is arguing that a timer set to finish counting in 2014 ought to finish in 1000 (or any other arbitrary year, for that matter) because there is a one-to-one correspondence between the numbers counted by the timer and whichever set of years you choose. But of course the one-to-one correspondence is just one of infinitely many correspondences between these sets, and the correspondence that’s actually expressed by the physical relationship of numbers counted by the timer and any particular set of years is one-to-one only for the set of years ending in the year 2014. For every other set of years, the expressed correspondence is not bijective, and conversely, the bijective function is not expressed. Here is the expressed correspondence between the numbers on the timer and years:
Function 1: t = f(y) = y – 2014 (with the adjustment described in footnote [36] for years BCE)
Timer: ... -4 -3 -2 -1 0 Years: ... 2010 2011 2012 2013 2014 2015 2016 ...
This function is bijective only for the set of years ending in 2014. For any set of years ending in 2015 or later, there are years that don’t correspond to any number on the timer. Similarly, for any set of years ending in 2013 or earlier, there are numbers on the timer that don’t correspond to any year in that set.
Here is another possible one-to-one correspondence between the counter and years:
Function 2: t = g(y) = y – 2013
Timer: ... -3 -2 -1 0 Years: ... 2010 2011 2012 2013 2014 2015 2016 ...
The physical arrangement for Function 2 differs from the physical arrangement for Function 1, since the counter finishes a year earlier. Similarly, there are bijective functions for each of the infinitely many other possible years in which the timer could finish, and each of them has a different physical arrangement. But Function 1 is the only one of these bijective functions that matches the physical arrangement of the actual timer. In other words, it’s the only one that’s expressed by the timer. Thus the timer finishes counting in 2014 and not in any other year.
Craig’s second argument similarly assumes the one-to-one correspondence between days and years must be expressed by their physical relationship. But of course the correspondence that’s actually expressed is 365-to-one.
[43] When I speak of adding a set of new elements to an existing set, I’m referring to an original set A, a nonempty disjoint set B consisting of the new elements to be added, and the resultant set C, which is the union of A and B. For the purposes of this discussion I will refer to this as a transition from A to C.
[44] If it’s possible that time existed before the universe, then it must be understood that time in these statements refers to that part of time that is coextensive with the universe.
[45] William Lane Craig, The Kalām Cosmological Argument, p. 63.
[46] If it’s impossible for a potential infinite to ever be an actual infinite, then it would seem the word potential is being misused. Nonetheless, the mathematical symbol ∞ is sometimes said to represent a potential infinite. It would be more accurate to say it represents the lack of an upper bound. And the real numbers (to which ∞ usually applies) lack an upper bound precisely because ℝ (the set of real numbers) is infinite, even though every real number is finite.
[47] Guminski makes a similar point in AG2.F82 when he says “the true propositions (i.e., the facts) about future events of an endless future (say in Heaven or Hell) are infinitely many, and hence an actual infinite.”
[48] William Lane Craig, The Kalām Cosmological Argument, pp. 200-201.
[49] William Lane Craig, The Kalām Cosmological Argument, p. 195.
Copyright ©2017 by Stephen Nygaard. The electronic version is copyright ©2017 by Internet Infidels, Inc. with the written permission of Stephen Nygaard. All rights reserved.



