(2019)
Stephen Nygaard
Introduction
Probability Concepts
Bayes’ Theorem
Life-Friendly Universes
The Main Theorem of IJ
Why IJ is Not Very Useful
What FTA Needs to Show
Other Criticisms of IJ
Vesa Palonen
Luke Barnes
The Application of Probability to Robin Collins’ FTA
The First Premise
The Second Premise
The Third Premise
The Conclusion
A Final Problem
Conclusion
Appendix
Notes
Introduction
A paper written over twenty years ago by Michael Ikeda and Bill Jefferys[1] proves a mathematical theorem purporting to show that a supernaturalistic explanation for the universe is not supported by the anthropic principle. The Ikeda-Jefferys thesis (IJ) is presented as a counterargument to the fine-tuning argument (FTA) and is based on a limited version of the weak anthropic principle (WAP). (A list of abbreviations used in this paper can be found in Table 4 in the Appendix.) Although the main theorem of IJ is undoubtedly correct, it is not a very useful argument against FTA, unlike other aspects of probability theory.
The “anthropic principle” is a name that has been applied to several different ideas, and WAP itself has more than one version. What they have in common is the assertion that the observed properties of the universe must be compatible with its observers, since otherwise the observers couldn’t exist. They differ primarily in what can be inferred from this assertion. Especially controversial is the claim that various properties of the universe are explained by the anthropic principle, or that it obviates the need for an explanation. The limited version of WAP used by IJ does not make such a claim.
Although the details of FTA may differ among authors, every version is based on the idea that certain fundamental physical constants[2] have values that make life possible, and if these values were even slightly different, then life could not exist. Moreover, the probability that all these constants would have precisely the values needed for life is vanishingly small, so small that it is virtually impossible that they occurred by chance, and therefore they must have been established by a supernatural creator, which is presumed to be God. In short, the standard premise (SP) of FTA is that fine-tuning is extremely improbable if naturalism is true. I have little doubt that a significant part of FTA’s appeal is its use of science to argue for theism.
This paper explains IJ, presents some criticisms of it, and examines some counterarguments to FTA based on probability theory, showing that IJ does not play a significant role among them. For the sake of argument, SP is assumed to be true since IJ and the other counterarguments presented here do not target SP. Moreover, if it’s false, FTA fails, making these counterarguments unnecessary.
Probability Concepts
Only a few basic concepts from probability theory are needed to understand IJ. If A is a true or false statement about an event, then the probability that A is true is written as P(A). For any A, it’s always the case that 0 ≤ P(A) ≤ 1. If P(A) = 0, then A is always false, that is, the event will never occur. If P(A) = 1, then A is always true, which means the event will always occur. If P(A) = 1/2, then A is equally likely to be true or false. A tilde (~) is used to negate a statement.[3] Thus ~A means A is false and P(~A) is the probability that A is false. Since A must be either true or false, P(A) + P(~A) = 1.
If you toss two dice (and to distinguish one from the other, assume one is red and the other is blue), each of the six possible values from the red die can combine with each of the six possible values from the blue die, giving 36 possible values for the total, as shown in Table 1. If A is the statement “The total from the two dice is 8,” then P(A) = 5/36 because 5 of the 36 cells in the table have 8 (shown in a red font) as the total, and each cell is just as likely as any other to be the total.
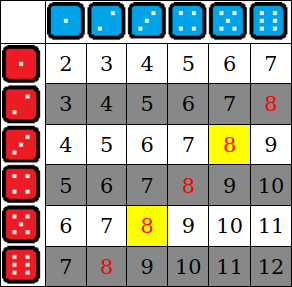
If you don’t see the result after tossing the dice, but you’re told the number on the red die is odd, then this information changes the probability that the total is 8 because it eliminates the gray rows as possible values for the total. Now only the 2 yellow cells out of the 18 nongray cells have 8 as the total, so the probability is 2/18 = 1/9.
This is an example of conditional probability. This is written as P(A|B), which can be read as “the probability of A given B.” In this example, B is the statement “The number on the red die is odd.” Conditional probability is defined as follows, where the ampersand (&) indicates both statements are true.[4]
| P(A|B) = | P(A&B) |
| P(B) |
In this example, P(A&B) = 2/36 = 1/18 because 2 of the 36 cells have 8 as the total with an odd number showing on the red die, and P(B) = 3/6 = 1/2, because 3 of the 6 possible values on the red die are odd. Thus P(A|B) = 1/18 ÷ 1/2 = 1/9.
Bayes’ Theorem
Bayes’ theorem is the following formula, derived from the definition of conditional probability:
| P(B|A) = | P(A|B)P(B) |
| P(A) |
P(B|A) is called the posterior probability. To continue with the preceding example, P(B|A) is the probability that the number showing on the red die is odd, given that the total on both dice is 8. Using Bayes’ formula and substituting the values we’ve previously calculated, we get P(B|A) = (1/9 × 1/2) ÷ 5/36 = 2/5. This is what we should expect because 2 of the 5 cells that have 8 as the total also have an odd number on the red die.
There is another form of the formula that is useful for determining which of two competing hypotheses is better supported by some given evidence. If h1 and h2 are the two hypotheses and e is the evidence, then the odds form of Bayes’ theorem is the following formula:
| P(h1|e) | = | P(h1) | × | P(e|h1) |
| P(h2|e) | P(h2) | P(e|h2) |
If the value computed by the formula is greater than 1, the evidence favors h1, while a value less than 1 favors h2. P(h1) and P(h2) are known as the prior probabilities, because they are the probabilities assigned to the hypotheses prior to taking the evidence e into account.
For example, suppose h1 is Newton’s theory of gravity and h2 is Einstein’s theory of gravity. For most events, both theories predict identical results, at least within the limits of our ability to measure. Consequently, the prior probabilities of both hypotheses must be about the same, so their ratio, which is the first term on the right, must be very close to 1, which essentially allows us to ignore that term. Notice we need to know only the ratio, not the individual values of the prior probabilities.
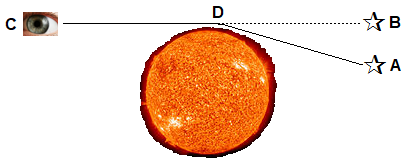
For the second term, we need something where the two theories predict different results. Einstein wrote that “a ray of light passing near a large mass is deflected.”[5] This is shown in Figure 1, in which the light from a star located at point A is deflected as it passes by the sun at point D. When the light reaches the observer at point C, it appears to the observer that the star is located at point B. Of course, the sun is far too bright for the star to be observed except during a total eclipse, when the sun’s light is blocked by the moon. Both theories predict the deflection, but Einstein’s theory predicts the angle will be twice what Newton’s theory predicts. As Einstein wrote, “The existence of this deflection, which amounts to 1.7” … was confirmed, with remarkable accuracy, by the English Solar Eclipse Expedition in 1919.”[6]
Figure 1: The Sun’s Gravity Bending the Light from a Star
Since the experimental measurement was much closer to Einstein’s prediction, it’s intuitively obvious that this is evidence in favor of his theory over Newton’s.[7] For various reasons, we don’t expect experimental results to match a prediction exactly. Consequently, experimental confirmation is not an “either/or” choice. Rather, there is a certain probability that a given result conforms to the theory’s prediction. The second term on the right side of the odds form of Bayes’ theorem is the ratio of this probability for the first hypothesis compared to the second hypothesis. We don’t have to know the actual probabilities in order to use the formula, only the ratio. In this case, the ratio is much less than 1 because the experimental result is much more probable on Einstein’s theory than on Newton’s.
One final remark about probability is appropriate: Although we have a well-developed and rigorous mathematical theory of probability that is an essential part of a wide range of practical applications, the meaning of probability remains unsettled. Especially controversial is the question of what it means, if anything, to talk about the probability of a single event in isolation.[8] If our universe is the only universe, then some answer to this question must be assumed in order to make SP meaningful, since it’s a probability statement that applies to a single universe viewed as a whole. Nonetheless, it is beyond the scope of this essay to discuss the various answers that have been proposed. Since I am assuming for the sake of argument that SP is true, I believe the reader’s intuitive sense of what the premise means will suffice for the purposes of this essay.
Life-Friendly Universes
Before proceeding to IJ, an explanation of the term “life-friendly” is in order. A universe is said to be life-friendly if and only if it is possible for life to develop in that universe naturalistically, without any sort of supernatural interference. It’s important to notice that the requirement is only that it’s possible. If life never develops in a universe, it can still be life-friendly, provided the conditions exist that make it a possibility, even though not an actuality.
A universe can also be life-friendly in spite of any amount of supernatural intervention, provided that intervention isn’t strictly necessary for the development of life. In a deistic universe, for example, God participates in its creation, but after that it operates exclusively according to naturalistic principles. A more “hands-on” deity might intervene repeatedly, but as long as life could have developed—at least in theory—without that intervention, such a universe counts as life-friendly.
The assumption that underlies SP is that the physical constants in a life-friendly universe must be fine-tuned because life is possible naturalistically only when these constants are restricted to a very small range of their possible values. If this underlying assumption is false, then FTA fails, and this entire discussion is superfluous. If it’s true, then “life-friendly” and “fine-tuned” may be considered synonymous.
The Main Theorem of IJ
IJ begins by noting that there are three attributes that a possible universe can have that are relevant to FTA, which are designated by the following letters:
| N: | The universe is naturalistic, that is, it’s governed solely by naturalistic laws with no supernatural influence. |
| F: | The universe is life-friendly. |
| L: | The universe actually has life. |
There are eight possible ways to combine these attributes, as shown in Table 2.
Any method of calculating the probabilities in the table will certainly be controversial, with one exception. It’s impossible for a naturalistic universe to have life if it’s not life-friendly because that would be a contradiction in terms. Consequently, there can be no NUL universes (shaded in red in the table). This means that P(NUL) = P(N&~F&L) = 0. It follows that P(F|N&L) = 1, that is, given that a universe is naturalistic and has life, it must be life-friendly. This is the limited version of WAP embedded in IJ. Since it’s a tautology, it should not be controversial.
Since our universe obviously has life, it can’t be any of the types shaded in gray. And since it’s impossible for any universe to be NUL, that leaves only SUL, SFL, and NFL as possible types for our universe. If naturalism is true, then it’s NFL. If theism is true, then it’s SUL or SFL. Advocates of Intelligent Design and other forms of creationism argue that life could not develop without supernatural intervention, which means our universe is not life-friendly and therefore must be SUL. Being fine-tuned, on the other hand, implies being life-friendly, so FTA argues that our universe is SFL.[9] From this we can see that FTA must show that our universe is much more likely to be SFL than NFL, that is, that P(SFL) >> P(NFL).[10]
This brings us to the main theorem of IJ, which is this:
| P(N|F&L) = | P(F|N&L)P(N|L) | = | P(N|L) | ≥ P(N|L) |
| P(F|L) | P(F|L) |
The first step is derived using Bayes’ theorem. The second step follows because P(F|N&L) = 1. The final step follows because 0 < P(F|L) ≤ 1. The main theorem shows that given that our universe has life, finding out that it’s life-friendly cannot make it less likely to be naturalistic.
Another way to look at is this: Since our universe has life, it must be SUL, SFL, or NFL. That means:
| P(N|L) = | P(NFL) |
| P(SUL)+P(SFL)+P(NFL) |
When we find out that our universe is life friendly, it eliminates the possibility that it’s SUL, which means:
| P(N|F&L) = | P(NFL) |
| P(SFL)+P(NFL) |
Now P(N|F&L) ≥ P(N|L) because P(SUL) ≥ 0. However, I suspect that most theists would deny that P(SUL) = 0 is possible because that would mean not just that Intelligent Design is false, but also that it’s impossible for God to create a non-life-friendly supernaturalistic universe with life. Since such a universe is not a logical contradiction, God’s inability to create one is inconsistent with omnipotence. Now if P(SUL) ≠ 0, then P(SUL) > 0, in which case P(N|F&L) > P(N|L). In other words, finding out that that a universe with life is life-friendly makes it more likely to be naturalistic. This makes sense because it eliminates only the possibility of a supernaturalistic type.[11]
Why IJ is Not Very Useful
I suspect a typical initial reaction to IJ is to wonder how it’s possible that discovering the universe is fine-tuned could fail to decrease the probability of naturalism if fine-tuning is extremely improbable given naturalism. The answer is that learning the universe is fine-tuned is distinct from learning that fine-tuning is extremely improbable given naturalism. IJ shows that the former cannot decrease the probability of naturalism. It doesn’t show that the latter cannot.
SP asserts that a naturalistic universe is highly unlikely to be fine-tuned, that is, P(FT|N) << 1, where FT stands for “the universe is fine-tuned.” If we assume SP is true, then FT is equivalent to F, that is, a fine-tuned universe and a life-friendly universe are one and the same, in which case SP is equivalent to P(F|N) << 1.
Imagine an extreme version of FTA whose basic premise is P(F|N) = 0, that is, it’s impossible for a naturalistic universe to be life-friendly. Call this EP, for “the extreme premise.” Then P(N|L&EP) = 0, that is, it would be impossible for a universe to be naturalistic if it has life and EP is true, since it would have to be life-friendly but can’t be. Now suppose that if P(F|N) increases very slightly above zero, then so does P(N|L&EP). Call this SIA, for “the small increment assumption.” Since increasing P(F|N) above zero means that EP turns into SP, it follows that P(N|L&SP&SIA) << 1. Neither SP nor SIA alters the main theorem of IJ, so P(N|F&L&SP&SIA) ≥ P(N|L&SP&SIA). In other words, even though learning F cannot reduce the probability of naturalism, it’s still highly improbable before learning F, given L, SP and SIA, and likely very improbable after learning F.
To avoid this, IJ must be supplemented to show at least one of three things, namely that SP is false, that SIA is false, or that P(N|F&L&SP&SIA) >> P(N|L&SP&SIA). Disproving SP would render IJ unnecessary. And it would be very difficult to prove or disprove SIA mathematically because the quantities involved are defined only vaguely. I do, however, think it’s possible to formulate an argument in conjunction with IJ to show that P(N|F&L&SP&SIA) >> P(N|L&SP&SIA), that is, although naturalism is highly improbable given L, SP and SIA, the probability increases greatly when also given F. But as I will explain, I also believe any such argument would be highly speculative and hence of little value.
What FTA Needs to Show
I said earlier that FTA needs to show that P(SFL) >> P(NFL). If SP is true, then a life-friendly universe must be fine-tuned, making this equivalent to showing that P(~N|FT&L) >> P(N|FT&L). Using the odds form of Bayes’ theorem is perhaps the easiest way to do this. The following shows the evidence and the competing hypotheses:
| e: | FT&L (The universe is fine-tuned and has life.) |
| h1: | ~N (The universe is supernaturalistic.) |
| h2: | N (The universe is naturalistic.) |
If we plug this into the odds form of Bayes’ theorem, we get:
| P(~N|FT&L) | = | P(~N) | × | P(FT&L|~N) |
| P(N|FT&L) | P(N) | P(FT&L|N) |
If this ratio is significantly greater than 1, then the evidence strongly supports supernaturalism over naturalism. Now SP asserts that P(FT|N) << 1. Since P(FT|N) = P(FT&L|N) + P(FT&~L|N), it follows that P(FT&L|N) ≤ P(FT|N) << 1. Thus, if SP is true, the denominator of the second term on the right side is very close to zero. Then to show the overall ratio is significantly greater than 1, FTA just needs to show that the product of the first term (the ratio of the prior probabilities of supernaturalism and naturalism) and the numerator of the second term (the probability that a supernaturalistic universe is fine-tuned and has life) is not nearly so close to zero.
Although IJ has limited value in countering FTA, it’s not completely useless. Since fine-tuning implies being life-friendly, finding out the universe is fine-tuned eliminates the possibility of a SUL universe, and this does increase the probability of naturalism. Unfortunately, IJ provides no way to determine the size of this increase.
Of course, even if FTA can show that the universe is much more likely to be supernaturalistic than naturalistic, this still falls short of showing that fine-tuning supports theism over naturalism. After all, theism is just one possible supernaturalistic hypothesis.
Other Criticisms of IJ
It’s just as important to understand what IJ does not assert as what it does. It does not in any way explain fine-tuning or show that fine-tuning does not need to be explained. Since there is no doubt that the math is correct, arguments against IJ tend to focus on its interpretation. I will examine two such criticisms.
Vesa Palonen
Vesa Palonen writes: “The fine-tuning of our universe’s fundamental laws and constants requires an explanation.”[12] He says that IJ treats the observation that our universe has life as background information, but this is illegitimate because “the probability of observation is not independent of the hypothesis but instead the observation is a probabilistic product of the hypothesis.”[13] In other words, if fine-tuning explains how it’s possible for life to exist, then it would be circular to argue that the existence of life explains fine-tuning. This criticism might be justified when directed against those who use the anthropic principle to make such an argument, but IJ is not among them—at least not explicitly.
Luke Barnes
Luke Barnes has developed a scenario based on John Leslie’s firing squad parable that specifically addresses IJ.[14] He imagines you’re sitting on a porch with your grandpa, who tells you he’s Magneto, a presumably fictional character who can telekinetically control metal. When you ask him to prove it, he levitates a set of keys a few inches above his above his hand, which you justly consider to be insufficient proof. Suddenly, a nearby explosion sends several tons of sharp metal shards towards the porch, all of which somehow miss both of you, but cover every inch of the house except for two silhouettes of you and your grandpa, who claims to have used his Magneto powers to alter the paths of the shards. Barnes then redefines the three properties of possible universes to fit this situation.
Barnes argues that since you’re alive, that means P(F|N&L) = 1, just as in IJ. Furthermore, since IJ shows that P(N|F&L) ≥ P(N|L), therefore “you cannot conclude anything at all about your Grandpa’s abilities. Observing that all the shards of metal missed my body has somehow made it not less likely that they simply followed ballistic paths from the explosion.” Barnes makes it clear that although this conclusion follows from IJ, he doesn’t believe it. His argument seems to be that IJ contradicts common sense, and therefore must be flawed, even if he can’t identify the flaw.
Although Barnes doesn’t explicitly define “you-friendly,” he clearly intends it to mean that all the shards miss you. But suppose a small number of them hit you in some nonvital spot but don’t kill you. In that case, P(F|N&L) ≠ 1, and the scenario is irrelevant to IJ. Redefining “you-friendly” to mean that you survive doesn’t help because then there would be no difference between F and L, again rendering the scenario irrelevant. To fix this problem we must amend the scenario. Let’s suppose that every shard is covered with a poison so lethal that the slightest contact is invariably and immediately fatal. Now if we define “you-friendly” to mean that all the shards miss you, then we have P(F|N&L) = 1.
There are four possible cases for whether the paths are normal or skewed, and friendly or unfriendly (meaning the shards miss or hit you, respectively), given that you survived, as shown in Table 3. Notice the NUL case is impossible because of the poison.
The SUL case is also impossible because of the poison, which means that P(N|F&L) = P(N|L). But suppose we change the scenario again to give Magneto the power to remove the poison when he deflects the shards so that if a few still hit you, they’re not necessarily fatal. Now we have P(SUL) > 0, which means that when you find out the shards have missed you, you can rule out that SUL has occurred, and its probability is then split proportionately between the two remaining cases, SFL and NFL.[15] In other words, P(NFL) increases, so P(N|F&L) > P(N|L).
Provided P(F|N&L) = 1, it’s always the case that P(N|F&L) ≥ P(N|L), just as IJ tells us. Therefore, it’s true that “Observing that all the shards of metal missed my body has somehow made it not less likely that they simply followed ballistic paths from the explosion.” But Barnes designed his scenario to make P(N|L) << 1, that is, the probability is extremely low that the shards traveled normal paths given that you’re alive. Finding out the paths were “you-friendly” either leaves this probability unchanged or increases it slightly. Either way, it remains extremely low. IJ does not somehow make it likely that the shards traveled normal paths.
Now what can you conclude about your grandpa’s abilities? Whether the shards traveled normal paths or not, if this were real and not a wild flight of the imagination, the result is so extraordinarily improbable that it would be only reasonable to ask for an explanation. And nothing in IJ denies this. But is the hypothesis that your grandpa is Magneto and he altered the paths of the shards a good explanation? Consider some alternative hypotheses:
- The Flash used his superspeed to deflect the shards so quickly that no one saw him.
- You and your grandpa were sprinkled with magic shard-repellent dust just before the explosion.
- Aliens from another planet used their advanced technology to save you so they could continue studying you and your grandpa.
Usually it makes no difference whether the hypothesis or the evidence comes first (except for how background knowledge is defined). But this is not the case for an ad hoc hypothesis, that is, one made for the sole purpose of explaining a given piece of evidence and nothing else. Magic dust is an ad hoc hypothesis because I clearly made it up just for this purpose. Although the Flash was created prior to and independently of this scenario, this is also ad hoc because it’s a statement about the Flash that I made up just for this situation. And the same holds true for aliens. Now these ad hoc hypotheses have virtually no credibility. If your grandpa had claimed to be Magneto after the explosion instead of before, this would also be ad hoc. As it is, it’s still a dubious hypothesis unless your grandpa provides additional evidence that he is indeed Magneto.
If this incident is the only evidence that we have for these hypotheses, which would be the best explanation of the four? Each one, if true, would mean you’re almost certain to survive. Consequently, the best hypothesis is the one with the greatest prior probability. But they all have remarkably low prior probabilities. Myself, I would be inclined to say that the probability of aliens is not nearly as low as that of comic book superheroes or magic dust. But since this scenario is highly contrived and unrealistic, who can say? What should be clear is that the reason these ad hoc hypotheses have so little credibility is that they have such low prior probabilities.
The alternative hypotheses I proposed are unworthy of serious consideration because there is no good reason to believe that the Flash or magic dust even exist, or that aliens have come to earth, let alone that any of them have done what the hypotheses assert. In contrast, the Magneto hypothesis could be verified, at least in the context of this unrealistic scenario, by having your grandpa use his powers under controlled conditions. If he proves he really is Magneto, that would explain how you survived the shards, but at the cost of creating even greater mysteries. It would almost certainly require radically new scientific theories to explain such powers.
On the other hand, if your grandpa provides no further evidence that he is Magneto, the most reasonable conclusion is that we don’t know why the shards followed the paths they did. This certainly doesn’t mean there’s no need to continue searching for an answer. But any explanation assumed beyond what reason and evidence can provide is almost certain to be wrong. Nor is this to say there’s something wrong with speculation. After all, discovering the explanation will almost surely begin with speculation. But it’s important to recognize that the value of speculation generally depends on the foundation on which it’s built, and even the most solid foundation doesn’t alter the fact that it’s just speculation.
The Application of Probability to Robin Collins’ FTA
Robin Collins’ exposition of FTA[16] has many virtues. Most notably, it’s comprehensive, thoroughly researched, and modest in its goals. These features make it a good choice for demonstrating how IJ and other probabilistic considerations apply even when SP, that is, P(FT|N) << 1, is assumed.
The First Premise
Collins’ first premise is P(LPU|NSU & k’) << 1 (p. 207), where k’ represents some appropriately chosen background information (which he explains at length on pp. 239-252), LPU (the existence of a life-permitting universe) is the same as FT (provided the evidence for the first premise shows, as I am granting, that F implies FT), and NSU (the naturalistic single-universe hypothesis) is (more or less) the same as N. In short, his premise differs from P(FT|N) << 1 in that he explicitly specifies appropriate background knowledge and limits the premise to the hypothesis that ours is the only universe. The former is a minor difference, and although the latter is not, he doesn’t ignore the multiverse hypothesis, which he says is “widely considered the leading alternative to a theistic explanation” (p. 203). On the contrary, he spends considerable effort arguing against it as a viable alternative (on pp. 256-272). Consequently, I will treat his first premise as equivalent to SP.
Of course, there are other objections that can be raised besides the multiverse hypothesis. For example, Victor Stenger has argued that the universe is not really fine-tuned at all, or at least not to an extent that makes it highly improbable.[17] Collins has also replied to Stenger’s objections (on pp. 222-225). It is beyond the scope of this essay to examine these and other arguments and counterarguments since I am assuming for the sake of argument that Collins’ first premise is true.
I should point out that Collins gives an answer to the question I raised about what it means to talk about the probability of a single event in isolation. Although it’s hardly surprising that his answer allows SP to be meaningful, he is to be commended for providing a thorough and extensive defense of it (see pp. 226-239).
The Second Premise
Collins’ second premise is ~P(LPU|T & k’) << 1 (p. 207), where T is the theistic hypothesis. In other words, it’s not highly improbable for the universe to be life-friendly if God exists. Collins is aware that just because making a life-friendly universe is a simple task for omnipotence, that in itself is not enough to show that its probability is not low. After all, just because I could easily gouge my eyes out doesn’t mean the probability of my doing it is not very close to zero. Collins points out that justifying this premise depends on finding “some reason why God would create a life-permitting universe over other possibilities” (p. 254). He says that “since God is perfectly good, omniscient, omnipotent, and perfectly free, the only motivation God has for bringing about one state of affairs instead of another is its relative (probable) contribution to the overall moral and aesthetic value of reality” (p. 254).[18] He then argues that embodied moral agents make such a contribution.
Collins assures us that there is “good reason to think that the existence of such beings would add to the overall value of reality” (p. 255). The good reason he cites is his belief that the existence of embodied moral agents results in a preponderance of good over evil. Given that we know about moral agents on only one tiny planet in a vast universe, this is a highly speculative assumption.[19] But more importantly, this is a remarkably low bar for omnipotence. Why would God settle for a mere preponderance when he surely could tip the balance overwhelmingly in favor of good? In fact, if God is perfect, wouldn’t the creation of any evil at all result in reality becoming imperfect, reducing the overall moral value of reality?
Given that most theists believe in an afterlife that is far superior to this earthly existence, why would God create this inferior universe? It can’t be because this universe has some attribute, such as free will, that is lacking in heaven. Even if this attribute is highly desirable but somehow incompatible with heaven, it doesn’t change the fact that the relative contribution of this universe is less than at least one alternative, and therefore, by Collins’ criterion, God should be motivated to create the alternative rather than this universe. Indeed, the criterion would seem to require God to follow Leibniz and create only the best of all possible worlds.
If we accept that God wants to create imperfect moral agents, does that explain why God would create a fine-tuned universe in which they can be embodied? First of all, Collins never explains why moral agents need to be embodied. This makes it appear that this attribute is there only as an excuse to avoid explaining why the universe is physical and not because it adds to the overall value of reality. Secondly, just because I want something to eat hardly makes it any less improbable that I will go to Joe’s Roadkill Diner and order the splattered skunk entrails platter if other options are available. There are surely a great many ways for omnipotence to create moral agents, embodied or otherwise. It’s incumbent upon Collins to explain why God chose this specific way.[20] If God is omnipotent, why make a fine-tuned, physical universe that appears to be naturalistic?
Since an omnipotent God could create and sustain life in a universe that is not life-friendly, IJ shows that discovering that our universe is life-friendly eliminates all the non-life-friendly possibilities, thereby increasing the probability of naturalism while decreasing the probability of supernaturalism. Unfortunately, IJ does not show how great an increase, nor whether naturalism was extremely improbable before the increase and remains so after. As I mentioned earlier, I think an argument could be made that even if naturalism is highly improbable before the increase, this is not the case after. Such an argument would require showing that P(SUL) >> P(SFL), since if supernaturalistic universes with life are extremely unlikely to be life-friendly, then P(SFL) may not be significantly higher than P(NFL). But because any assertion about supernaturalistic universes must be based on unverifiable speculation, I doubt the attempt would be worthwhile.
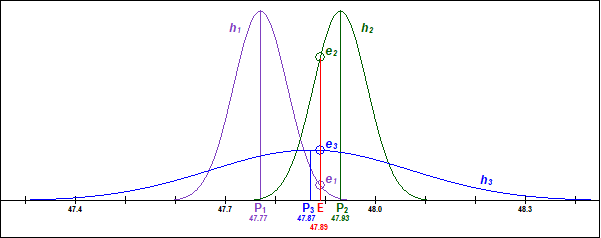
There is a much more serious difficulty with the second premise. Recall that experimental results are not expected to match predicted results exactly. This is illustrated in Figure 2, which shows (at the bottom) the predicted results P1 = 47.77, P2 = 47.93 and P3 = 47.87 for the three hypotheses h1, h2, and h3, respectively, and the experimental result E = 47.89. The vertical magenta line is located at the predicted value P1, and the magenta curve falling away on either side of it represents the probability that an experimental result supports h1. The vertical red line is located at the actual experimental result E, and it intersects the magenta curve at e1 (marked by the small magenta circle). This is a low point on the curve, indicating a low probability that E supports h1. In contrast, it intersects the green curve at e2 (marked by the small green circle), a much higher point indicating a high probability that E supports h2. Similarly, it intersects the blue curve at e3 (marked by the small blue circle) close to its peak, indicating a high probability (relative to the peak of the blue curve) that E supports h3. But e3 is still much lower than e2 because the blue curve is spread over a much wider range than the green curve.[21] Consequently, E supports h2 much more strongly than h3, even though E is closer to P3 than to P2. If we ignore h2 and compare only h1 and h3, we see that even though E gives stronger support to h3, that support is still weak. Hypotheses like h3 are not strongly supported by any specific result because the probability curve, being so spread out, never rises very high.
Figure 2: Probability curves for 3 hypotheses
Now does T have a broad or narrow probability curve? Consider the following questions: Does T predict the earth is flat or round? Does it predict the sun revolves around the earth or the earth around the sun? Does it predict that life requires supernatural intervention or that the universe is life-friendly? Now clearly T has failed in the past to predict the correct answers to these and a great many other questions that science has since answered. Either this is overwhelming evidence against T, or if T is allowed to make multiple, mutually inconsistent predictions, then T suffers from what I would call predictive inefficacy. A hypothesis is predictively ineffective with respect to an event if virtually any outcome for that event is consistent with the hypothesis. Such a hypothesis has a probability curve so broad that it cannot reliably predict anything about the event.
On the other hand, if a hypothesis doesn’t predict anything at all, but merely comes up with explanations after the fact, then it’s a fortiori predictively ineffective. T has certainly never predicted any specific value for any of the fine-tuned constants, or even that there are such constants. Moreover, Collins’ assertion that God wanted to create embodied moral agents is not presented as a prediction. Although Collins frequently uses the word “predict” (and its variants) when discussing scientific theories, he never uses it in reference to T. This leaves the impression that his second premise is little more than the vacuous claim that the world is how it is because God made it that way. This impression is reinforced by that fact that T explains so little. It is utterly useless for advancing scientific knowledge, or any kind of empirical investigation. The second premise is plausible in the trivial sense that fine-tuning is compatible with T. But because T is so predictively ineffective, virtually anything is compatible with it. Consequently, the probability that fine-tuning (or anything else) supports T is extremely low.
The Third Premise
Collins’ third premise is “T was advocated prior to the fine-tuning evidence (and has independent motivation)” (p. 207). In other words, T is not an ad hoc hypothesis. Now the existence of extraterrestrial aliens was certainly advocated before Luke Barnes came up with his scenario, and with independent motivation, and thus the hypothesis that aliens exist is not ad hoc. Yet the hypothesis that aliens intervened to save you and your grandpa is ad hoc because it goes well beyond the hypothesis of their existence. It imputes motives, abilities and actions to aliens that cannot be inferred from their existence, and for no other reason than to explain this intervention.
Aliens capable of traveling to earth would surely have technology advanced far beyond what we primitive earthlings possess. Because almost anything could be explained as the product of a sufficiently advanced technology, the hypothesis of aliens tends to be predictively ineffective. For this very reason, invoking it to explain any specific event is likely to be ad hoc. Similarly, since omnipotence is essentially advanced technology taken to its extreme limit, invoking T to explain any specific event, such as fine-tuning, is likely to be ad hoc even if T itself is not.
In his justification for his second premise, Collins gives a reason why God would want to create moral agents, but he fails to explain why these agents must be embodied in a fine-tuned universe. If he were advocating for naturalism, then he could argue that moral agents couldn’t exist without fine-tuning, and they must be embodied because the universe is physical. But since a universe created by a supernatural being is supernaturalistic by definition, the most a theist can argue is that God has made the universe appear to be naturalistic.[22] If God is omnipotent, then moral agents only appear to need fine-tuning. Even if Collins can provide some reason why God would create a fine-tuned physical universe that appears to be naturalistic, his third premise would still fail unless he can also show that he did not invent this reason solely to bolster his second premise.
The Conclusion
Collins’ conclusion is “Therefore, by the restricted version of the Likelihood Principle, LPU strongly supports T over NSU” (p. 207). The likelihood principle states that “e counts in favor of h1 over h2 if P(e|h1) > P(e|h2)” (p. 205). The restricted version of the likelihood principle simply disallows ad hoc hypotheses, which is the reason for the third premise. In a footnote, Collins says: “The Likelihood Principle can be derived from the so-called odds form of Bayes’s Theorem” (p. 205n2). Note that the likelihood principle assumes the prior probabilities of the two hypotheses can be ignored. But this is true only if their ratio is very close to 1. This was the case when we compared Newton’s law of gravity with Einstein’s. Disallowing ad hoc hypotheses eliminates one type of case where this assumption is wrong, but not all such cases. And if the assumption is wrong, the likelihood principle becomes useless. To see why, consider the following scenario.
Company X uses a number of machines with a component that must be periodically replaced. Accordingly, Company X keeps an inventory of these components, 96% of which come from Company A, and the other 4% from Company B. A component from Company B is four times more likely to fail within the first two weeks of operation than a component from Company A. Let the following be the evidence and competing hypotheses:
| e: | A component from inventory that was installed less than two weeks ago has failed. |
| h1: | The component is from Company A. |
| h2: | The component is from Company B. |
Clearly neither hypothesis is ad hoc. Since we are given that P(e|h2) = 4 × P(e|h1), according to the likelihood principle, e is four times more probable under h2 than h1, that is, the failed component is four times more likely to come from Company B. But this ignores the prior probabilities, namely P(h1) = 0.96 and P(h2) = 0.04. If we plug these values into the odds form of Bayes’ theorem, we get P(h1|e) = 6 × P(h2|e), that is, the failed component is six times more likely to come from Company A, contrary to the likelihood principle.[23]
The question then is whether the prior probabilities of naturalism and theism are approximately equal. Collins admits that prior probabilities cannot simply be ignored when he says: “In order to show that any hypothesis is likely to be true using a likelihood approach, we would have to assess the prior epistemic probability of the hypothesis, something I shall not attempt to do for T” (p. 208). As I pointed out, the odds form of Bayes’ theorem does not require us to know the prior probabilities of the competing hypotheses, only their ratio. Collins tries to evade the problem by arguing that “in everyday life and science we speak of evidence for and against various views, but seldom of prior probabilities” (p. 208). In other words, Collins’ justification for ignoring prior probabilities is that doing so is typical. It may be typical, but it’s also a cognitive blind spot. As Massimo Piatelli-Palmarini writes: “[N]one of us is, spontaneously or intuitively, a Bayesian subject. We have to learn at least some rudiments of statistics to modify our intuitions. The trouble is that as Tversky, Kahneman, and many others have shown, even professional scientists and statisticians can be induced into error.”[24]
Now consider that it has been four centuries since Galileo first mounted his defense of the Copernican system. In that time, not once has any supernaturalistic hypothesis found scientific success. On the contrary, the failure of supernaturalism is so complete that it has been effectively banished from science, with the sole exception of parapsychology, which is still struggling to achieve acceptance as a real science. Consequently, any probability assigned to naturalism that is not extremely high and any assigned to supernaturalism that is not extremely low is simply inconsistent with science.
There is another cognitive blind spot known as the conjunction effect. For example, suppose you’re given the following brief description of Bill: “Bill is 34 years old. He is intelligent, but unimaginative, compulsive, and generally lifeless. In school, he was strong in mathematics but weak in social studies and humanities.” You’re then asked to rank, from most to least likely, a list of eight items naming professions and hobbies that might apply to Bill. Five of the items are irrelevant, presumably included just to obscure the relevant items, which are:
| A: | Bill is an accountant. |
| J: | Bill plays jazz for a hobby. |
| A&J: | Bill is an accountant who plays jazz for a hobby. |
If you’re like most people, you rank A first among the relevant items, J last, and A&J somewhere in between.[25] But A&J cannot rank ahead of J because no matter what A and J are, P(J) = P(A&J) + P(~A&J), which means P(J) ≥ P(A&J). In this example, the probability that Bill plays jazz is equal to the probability that he is an accountant and plays jazz plus the probability that he is not an accountant and plays jazz, and therefore the probability of playing jazz cannot be less than either of those conjoined probabilities.
Now consider Collins’ definition of T: “there exists an omnipotent, omniscient, everlasting or eternal, perfectly free creator of the universe whose existence does not depend on anything outside itself” (p. 204). His argument, if successful, does not establish that T has any of the attributes given in the definition other than being the creator of the universe. Because he has conjoined this one attribute with five others, only a fraction of the probability he ascribes to T really belongs to T, with the rest belonging to the 31 alternatives that have contrary values for one or more of these other attributes. Each of these alternatives (excluding those that are logically impossible, if any) diminishes the probability of T as defined by Collins. Consider the alternative where the creator lacks all five attributes. What would such a creator be like?
One possibility is that it could be the cosmic equivalent of a computer programmer who has created the universe as a computer simulation.[26] Call this hypothesis CS. Are there any reasons to prefer CS over T? CS explains fine-tuning at least as well as T. Furthermore, there may be no way to know whether the programmer created the simulation in order to produce moral agents, although simulating an entire universe seems wasteful when a much smaller simulation could easily accommodate such beings. We could well be an unintended side effect of the simulation. Indeed, the appurtenances of a naturalistic universe—its indifference to individual moral agents, the long slow process of evolution to produce them, the biological imperfections resulting from that process—all seem far more compatible with CS than T. Moreover, this universe could be one of any number of simulations, many—even most—of which could be lifeless. Since FTA (if successful) establishes a conclusion with which both CS and T are compatible, the probability that would otherwise belong to T alone must be shared with CS, and possibly other alternative hypotheses, reducing the probability of T by at least half, if not much more.[27]
A Final Problem
Ultimately, the problem with FTA is that T is not a scientific explanation, which Collins admits when he says: “Rather, God should be considered a philosophical or metaphysical explanation of LPU” (p. 225). Since fine-tuning is a scientific problem, it’s unclear why we should be satisfied with anything other than a scientific explanation, or even how something merely philosophical or metaphysical can replace a scientific explanation. Collins seems to think a scientific explanation is ultimately not possible because “even if the fine-tuning of the constants of physics can be explained in terms of some set of deeper physical laws, as hypothesized by the so-called ‘theory of everything’ or by an inflationary multiverse, this would simply transfer the improbability up one level to the existence of these deeper laws” (p. 205). But his argument depends on his contention that the range of values that is life-permitting for each of the various constants is very small compared the range of possible values. How can he know this will be true of some as yet undiscovered deeper laws?
Consider that in the nineteenth century we knew from geology that the earth is several billion years old. We also knew that the energy received from the sun has been fairly constant during most—if not all—of that time. But there is no chemical reaction known then or now with that level of energy output that could be sustained at a nearly constant rate in a body the size of the sun for more than a small fraction of that time. No nineteenth century physicist could have foreseen the radical advances in physics needed to explain how the sun shines because of nuclear fusion. Anyone in the nineteenth century who attempted preemptively to circumscribe that explanation would almost certainly have been wrong. Likewise, although it’s possible that new theories will never resolve the issue of fine-tuning, how can anyone know that before those theories emerge?
Although I assumed for the sake of argument that Collins’ first premise is true, I believe he falls far short of proving it. Even if it’s granted that fine-tuning is so improbable that it cannot plausibly have occurred by chance, this doesn’t establish his first premise unless he also demonstrates that because science cannot currently explain fine-tuning, therefore naturalism explains it as a random occurrence. But other than asserting that deeper laws would simply transfer the improbability up one level, Collins makes no real effort to show this.
The notion that naturalism must invoke chance to explain why the universe is life-friendly is reminiscent of claims made by opponents of evolution who took the following sentence from Julian Huxley out of context: “One with three million noughts after it is the measure of the unlikeliness of a horse—the odds against it happening at all.”[28] The point Huxley was making, and which is very clear in context, is that the existence of the horse is extraordinarily improbable without natural selection. By quoting this out of context, the opponents of evolution attempted to create a binary choice: Either the existence of the horse is the absurdly unlikely result of chance, or it’s God’s handiwork. Similarly, proponents of FTA want to make it seem that chance is the only possible naturalistic explanation for fine-tuning, since if not, SP collapses, and FTA with it.
To be fair, Collins is not taking scientists out of context. Yet if fine-tuning stands in need of an explanation, the fact remains that at present we have only conjecture. But T hardly even counts as conjecture. Why, for example, are the relative strengths of the fundamental forces what they are? If some future scientific theory answers this question, it will make specific, testable mathematical predictions. Very likely it will lead to new technologies. No one expects anything of the sort from T. T did not predict fine-tuning, nor is there anything about T that would lead us to believe our universe is fine-tuned if science didn’t tell us so. And we certainly have no reason to expect T to explain the relative strengths of the fundamental forces in a way that would be mathematically accurate, or even marginally useful. We do not expect such knowledge to come from anywhere but science.
Conclusion
Although IJ is mathematically correct, other aspects of probability theory are much more useful in countering FTA. I mentioned IJ in only one place when applying probability theory to Robin Collins’ FTA, and even there its value is minimal. IJ proves that fine-tuning cannot decrease the probability of naturalism. And unless FTA admits that God could not create a non-life-friendly universe with life (presumably by denying his omnipotence), it actually increases it. However, IJ does not show how great an increase, nor whether naturalism was highly improbable before the increase and remains so after. Consequently, Bayes’ theorem, particularly the odds form of it, and other elements of probability theory are far more helpful in uncovering the shortcomings of FTA.
Even if naturalism cannot explain fine-tuning, theism in not a better alternative. FTA ultimately fails because theism is not an explanation at all in any practical sense. There is no chance that FTA or arguments like it are going to persuade scientists to abandon naturalism in favor of theism in their quest to uncover the mysteries of the universe and fine-tuning in particular. If there is a better alternative to naturalism, it will have to be something that bears even greater scientific fruit, not something that is merely philosophical or metaphysical.
Appendix
The following table lists the various abbreviations used in this paper with links to where they are defined.
| Abbr. | Definition |
|---|---|
| CS | The Computer Simulation hypothesis. |
| EP | The Extreme Premise. (The basic premise of the extreme version of FTA.) |
| F | The universe is life-friendly. |
| F | The paths are “you-friendly.” (In Luke Barnes’ scenario) |
| FT | The universe is fine-tuned. |
| FTA | The Fine-Tuning Argument. |
| IJ | The Ikeda-Jefferys thesis. |
| k’ | Appropriately chosen background knowledge. (Defined by Robin Collins) |
| L | The universe has life. |
| L | You are alive. (In Luke Barnes’ scenario) |
| LPU | The existence of a Life-Permitting Universe. (Defined by Robin Collins) |
| N | The universe is naturalistic. |
| N | The shards followed normal paths. (In Luke Barnes’ scenario) |
| NFL | The universe is Naturalistic, Friendly, and has Life. |
| NFL | The paths are Normal, Friendly, and you Live. (In Luke Barnes’ scenario) |
| NSU | The Naturalistic Single Universe hypothesis. (Defined by Robin Collins) |
| NUL | The universe is Naturalistic, Unfriendly, and has Life. |
| NUL | The paths are Normal, Unfriendly, and you Live. (In Luke Barnes’ scenario) |
| SFL | The universe is Supernaturalistic, Friendly, and has Life. |
| SFL | The paths are Skewed, Friendly, and you Live. (In Luke Barnes’ scenario) |
| SIA | The Small Increment Assumption. |
| SP | The Standard Premise of FTA. |
| SUL | The universe is Supernaturalistic, Unfriendly, and has Life. |
| SUL | The paths are Skewed, Unfriendly, and you Live. (In Luke Barnes’ scenario) |
| T | The Theistic hypothesis. (Defined by Robin Collins; full definition here) |
| WAP | The Weak Anthropic Principle. |
Notes
[1] Michael Ikeda and Bill Jefferys, “The Anthropic Principle Does Not Support Supernaturalism” in The Improbability of God ed. Michael Martin and Ricki Monnier (Amherst, NY: Prometheus Books, 2006): 150-166.
[2] An essential part of FTA is the notion that these constants are not really constant at all—that each one can have any value in some unspecified range. If this is true, it would be more accurate to call them “parameters” or “variables.” Many versions of FTA argue that the initial conditions of the universe and the laws of nature are also fine-tuned. For convenience, I will use the term “constant” with the understanding that this term may refer to something that is not necessarily a fixed constant.
[3] Sometimes other symbols (such as ¬) are used instead of a tilde. Whatever symbol is used, it can be read as the word “not.”
[4] If S is the set of cells in the table for which A is true, and T is the set for which B is true, the set for which A&B is true is S∩T.
[5] Albert Einstein, The Meaning of Relativity (New York, NY: MJF Books, 1922), p. 93.
[6] Einstein, The Meaning of Relativity, p. 93. The angle in the figure is obviously greatly exaggerated. If the angle were actually drawn as 1.77″, in order to separate points A and B by just 1 millimeter (0.04 inches), the distance from B to D would have to be just over 116.5 meters (382.2 feet).
[7] Arthur Stanley Eddington, the astronomer who led the expedition that Einstein cites, did not really confirm Einstein’s prediction. It is considered confirmed because more reliable measurements, taken after the publication of Einstein’s book, have consistently been similar to what Eddington achieved accidentally. As Michael Shermer put it, “It turns out that Eddington’s measurement error was as great as the effect he was measuring” (Why People Believe Weird Things: Pseudoscience, Superstition, and Other Confusions of Our Time. New York, NY: Henry Holt and Company, 2002, p. 301).
[8] For example, consider a weather forecast predicting rain. If it predicts a 0% chance and it rains, or a 100% chance and it doesn’t rain, then the prediction was wrong. But if it predicts any percentage in between, what would make the forecast right or wrong? For example, if the forecast predicts a 90% chance and it doesn’t rain, does that mean that the prediction was wrong? If so, then what’s the difference between a 90% chance and 100% chance? On the other hand, if the prediction was right, then what’s the difference between 90% and any smaller percentage? Is it even possible to answer these questions about this one prediction by itself, or must it be considered in conjunction with other predictions and their outcomes?
[9] This raises the question of whether it’s inconsistent for someone to advocate for both intelligent design (ID) and FTA, for the former argues that the universe is SUL while the latter assumes that it’s SFL. I don’t think that this is necessarily inconsistent. ID is false if the universe is life-friendly. Conversely, naturalism is false if it’s not life-friendly. But while FTA also assumes that the universe is life-friendly, FTA proponents would be perfectly happy if this turns out to be wrong, for that would falsify naturalism. So they can claim to be assuming that the universe is life-friendly simply for the sake of argument, and not because they necessarily believe that the assumption is true. Moreover, ID could be modified to assert that God made an SFL universe and then unnecessarily intervened. However odd this may be, it’s not a logical contradiction.
[10] Two consecutive greater than signs (>>) mean “is much greater than.” This is one of the few mathematical symbols that allow for vagueness since there is generally no precise cutoff between merely “greater than” and “much greater than.” Moreover, where the gray area lies is a matter of convention, which can vary greatly with the context. Later in this essay I will use expressions like P(A) << 1, which, in the context of probability, means that P(A) is very close to 0.
[11] For example, suppose all three types are equally likely given that the universe has life, that is, that P(SUL|L) = P(SFL|L) = P(NFL|L) = 1/3. Note this means that P(~N|L) = 2/3 and P(N|L) = 1/3, that is, that there’s a 2/3 chance that the universe is supernaturalistic. Then if we find out that the universe is life-friendly, we have P(SUL|F&L) = 0, and P(SFL|F&L) = P(NFL|F&L) = 1/2. Note that this means that P(~N|F&L) = P(N|F&L) = 1/2. In other words, the probability that the universe is supernaturalistic has decreased from 2/3 to 1/2, and the probability that it’s naturalistic has increased from 1/3 to 1/2.
[12] Vesa Palonen, “Bayesian Considerations on the Multiverse Explanation of Cosmic Fine-Tuning.” Preprint arXiv: 0802.4013 (2009), p. 2.
[13] Palonen, “Bayesian Considerations on the Multiverse Explanation of Cosmic Fine-Tuning,” p. 7.
[14] Luke Barnes, “What Do You Know? A Fine-Tuned Critique of Ikeda and Jefferys (Part 2)” (November 5, 2010). Letters to Nature blog. <https://letterstonature.wordpress.com/2010/11/05/what-do-you-know-a-fine-tuned-critique-of-ikeda-and-jefferys-part-2/>
[15] When I say that it’s split proportionately, I mean that the ratio of P(SFL) to P(NFL) remains the same. For example, if SFL was a trillion times more probable than NFL before you found out that the shards have missed you, it remains a trillion times more probable afterward, although both probabilities have increased.
[16] Robin Collins, “The Teleological Argument: An Exploration of the Fine-Tuning of the Universe” in The Blackwell Companion to Natural Theology ed. William Lane Craig and J. P. Moreland (Malden, MA: Blackwell, 2009): 202-281. From this point onward, page numbers in parentheses refer to this source.
[17] Victor Stenger, The Fallacy of Fine Tuning (Amherst, NY: Prometheus Books, 2011).
[18] Collins attributes this observation to Richard Swinburne, The Existence of God (Oxford, UK: Oxford University Press, 2004), pp. 99-106.
[19] Rather than shouldering the burden of proof by giving reasons to think that any moral agents populating the rest of the universe are predominantly good, Collins weakens his standard by arguing that if “we lack sufficient reasons to think that a world such as ours would result in more evil than good,” this would still be enough to support his thesis (p. 255). Instead, he puts the burden of proof on the atheist to “show that it is highly improbable that God would create a world which contained as much evil as ours” (p. 256).
[20] See Aron Lucas, “Review of The Blackwell Companion to Natural Theology” (2018) on the Secular Web for a fuller explanation of why this is a problem.
[21] Since the theoretical range of all three curves is infinite, it would be more accurate to say that the blue curve has a much larger standard deviation. When I speak subsequently of broad and narrow probability curves, I mean probability distributions with large and small standard deviations, respectively.
[22] This raises a question for proponents of FTA: Why would God deceive us by making the universe appear to be naturalistic? Of course, it would be the rare theist who would accept such an idea. Most would surely agree with René Descartes in saying, “I recognize that it is impossible that He should ever deceive me, since in all fraud and deception there is some element of imperfection. The power of deception may indeed seem to be evidence of subtlety or power; yet unquestionably the will to deceive testifies to malice and feebleness, and accordingly cannot be found in God” (“Meditation IV” of Meditations on First Philosophy in The European Philosophers from Descartes to Nietzsche ed. Monroe C. Beardsley. New York, NY: Random House, 1960: 25-79, p. 54). The question then becomes: Why is making the universe appear to be naturalistic not deceptive?
[23] If this seems counterintuitive, assume arbitrary values and see where it leads. For example, suppose 0.5% of components from Company A will fail within two weeks, and there are 10,000 components in inventory. Then 9,600 (96%) of the components are from Company A and 48 (0.5%) of them will fail, while 400 (4%) are from Company B and 8 (2%, which is 4 × 0.5%) of them will fail. A randomly selected component that fails is 6 times more likely to be one of the 48 from Company A than one of the 8 from Company B.
[24] Massimo Piatelli-Palmarini, Inevitable Illusions (New York, NY: John Wiley and Sons, 1994), p. 114.
[25] Piatelli-Palmarini, Inevitable Illusions, pp. 64-65. My own guess (and it’s just a guess) as to why most people rank A&J in the middle is that A is seen as consistent with the brief description and therefore is considered positive, while J is seen as inconsistent and hence negative. The A&J item is thus viewed as a combination of a positive and a negative, which tend to cancel each other out, with J pulling A toward the negative, and A pulling J toward the positive.
[26] I do not mean “simulation” in the usual sense, such as the sense described in the Wikipedia article “Simulation Hypothesis,” where the simulation is essentially a copy of the real world. This would be of no help in explaining fine-tuning. Rather, I mean that the simulation (where we exist) need not bear any resemblance to the real world (where the programmer exists). Interpreted in this way, we in the simulation might have no way of knowing any of the properties of the real world—or even that our universe is a simulation—unless the programmer chooses to communicate that information to us. The simulated world is supernaturalistic in the sense that it depends upon something outside of itself. But while God is clearly a supernatural being, the programmer may not be, for the real world in which the programmer exists could be naturalistic. However, if this is the case then the simulation is a naturalistic element of a naturalistic world, and thus it would probably be inappropriate to view this as a supernaturalistic hypothesis.
[27] An obvious objection to CS is to ask what evidence could possibly confirm or falsify it. The evidence of fine-tuning tends to support it in the sense that the probability of fine-tuning is high given CS, but that fact must be balanced against the prior probability of CS, which seems difficult—if not impossible—to assess. But this objection applies to T at least as much as it applies to CS. Moreover, when comparing CS and T, any assignment of probabilities is likely to be highly subjective.
[28] Julian Huxley, Evolution in Action (New York, NY: Mentor Books, 1953), p. 42. The phrase “One with three million noughts after it” refers to odds of 1 in 1,0001,000,000 that a million mutations would occur purely by chance with each mutation having one chance in a thousand of being favorable. The remainder of the paragraph reads: “No one would bet on anything so improbable happening; and yet it has happened. It has happened, thanks to the workings of natural selection and the properties of living substance which make natural selection inevitable” (p. 42).
Copyright ©2019 by Stephen Nygaard. The electronic version is copyright ©2019 by Internet Infidels, Inc. with the written permission of Stephen Nygaard. All rights reserved.



