---

The standard view of philosophers is that the existence of particular events within our universe is capable of being explained in terms of initial conditions and natural laws, but that the existence of our universe itself is a ‘brute given’ that is incapable of naturalistic explanation. A supernatural explanation of the existence of our universe may be alleged to be possible (‘God created our universe so that humans may exist and the existence of humans is an intrinsic good’), but an explanation that appeals only to factors, situations or regularities in nature is deemed to be in principle impossible. It is also a standard view of philosophers that the less fundamental natural laws of our universe are capable of being explained in terms of more fundamental laws of our universe, but that the most basic natural laws of our universe are incapable of being explained naturalistically. Perhaps they can be explained supernaturally, by asserting that God ordained them so that humans may eventually evolve, but no other explanation is supposed possible.

I believe these standard views are unduly conservative and that a naturalistic explanation of the existence and basic laws of our universe is possible. By this I mean that there is at least one model or type of explanation such that it is logically possible for there to be instances of this type that provide naturalistic explanations of the existence and basic laws of our universe. The type of explanation I have in mind is employed frequently in Quantum Mechanical accounts of microscopic events in our universe. Numerous events are explained by Quantum Mechanics in the sense that they are subsumed under laws that show these events are to be expected with a precise degree of expectation. These explanations are not causal explanations in the sense that their premises involve references to sufficient conditions of the events to be explained, but are statistical explanations in the sense that they state the frequencies (which may be low) with which the events occur in situations of a certain sort. Explanations of spontaneous radioactive decays are paradigmatic examples of explanations of this sort. For example, when an alpha particle in the nucleus of a U²³⁸ atom approaches the potential barrier that is the wall of the nucleus, the particle has a probability of 10^-38 of tunnelling through the barrier. ‘Tunnelling’ has a special meaning in Quantum Mechanics; something tunnels through a barrier if it spontaneously acquires for a certain period of time the extra energy it needs to pass through the barrier. There is no sufficient condition of the tunnelling of the alpha particle through the wall of the nucleus, but this tunnelling is explained in the sense that it is subsumable under the following statistical law:

(1) P(T/A) = 10^-38

where ‘P’ stands for probability and

T = the spontaneous tunnelling of an alpha particle through the wall of the nucleus of a U²³⁸ atom, and

A = the approach of an alpha particle to the wall of the nucleus.

(1) says, in effect, that the probability of an event of the T sort (tunneling through the wall) being associated with an event of the A sort (approaching the wall) is 10^-38. Accordingly, if a certain alpha particle x tunnels through a barrier, then its tunnelling can be accounted for by the following inductive inference:

(1) P(T/A) = 10^-38

(2) Ax

________

________ [10^-38]

(3) Tx

(2) says that the alpha particle x has the property A, the property of approaching the wall of the nucleus of a U²³⁸ atom. (3) asserts that the particle x has the property T of tunnelling through the wall. The double line indicates that (1) and (2) make probable (3) and ‘[10^-38]’ indicates the degree to which they make (3) probable.

(1)-(3) illustrates the type of explanation I shall use in my constructions of logically possible explanations of the existence and basic laws of our universe. One premise will state a statistical law, another that a certain particular has a certain property, and the conclusion will state (or at least imply) that our universe exists or that the basic laws of our universe obtain.

The type of explanation I shall use bears some affinities to Hempel’s I-S (inductive-statistical) model of scientific explanation. The main difference between Hempel’s I-S model and the model I shall use is that Hempel supposed that I-S explanations require the explanandum-statement to be made highly probable by the explanans-statements, whereas the model I use does not require this.¹ I agree with W. Salmon, R. Jeffries, P. Railton and others² that high probability is not a necessary condition of statistical explanations. But it should not go unremarked that Hempel subsequently came to acknowledge this and in 1976 proposed a new version of I-S explanations which allows low probabilities.³ I shall call this new version the neo-I-S model of explanation and shall use this model in the construction of my cosmological explanations. It will not be necessary for the limited purposes of this paper to take a stand vis à vis the other modifications to Hempel’s original I-S model that have been proposed in the literature,⁴ but it is crucial to my project to affirm that the neo-I-S model retain an essential feature of the original I-S model, that the explanations must establish a nomic expectability of the item mentioned in the explanandum-statement but need not casually explain it.⁵ The explanans-statements need not cite factors that cause the explanandum-item but merely need to establish that this item is to be expected (which in the new model may be a low expectability). As is well-known, this view of statistical explanation has recently been opposed at some length by Salmon. In his new book Salmon develops a broad-based theory of probabilistic causality and argues that the explanans-statements must cite a cause (which need not be a sufficient condition) of the explanandum-item. According to this theory, the approach of an alpha particle to the wall of the nucleus of a U²³⁸ atom is a causal process that has the propensity of 10^-38 to bring about or undergo a tunnelling through the wall and by virtue of this fact its tunnelling through the wall (if it occurs) has a causal explanation. It is not necessary for my purposes to counter Salmon’s arguments that explanations of particular events within the universe must be causal, but it is necessary to show that his arguments do not apply to explanations of the existence and basic laws of our universe. I will argue in Section 4 that causal references are neither possible nor requisite for natural explanations of the existence and basic laws of our universe. Causal references are not possible since any alleged natural cause of the universe, even if construed in accordance with Salmon’s liberal criteria of causes, would really be a part of the universe and thereby would be among the phenomena that need to be explained. I will show, secondly, that the absence of causal references is not sufficient to deprive my cosmological arguments of explanatory value; specifically, I will demonstrate that my cosmological subsumptions do not possess all the defining features Salmon associates with acausal subsumptions that have little or no explanatory value and therefore that my cosmological subsumptions fall outside of his category of acausal subsumptions that are not (genuine) explanations.

The primary aim of the following sections is to contravene the traditional assumption, recently articulated by Richard Swinburne, that ‘there can be no scientific [naturalistic] explanation of the existence of a universe; for all that science can do is to explain how a present state of the universe was brought about by a past state, It cannot explain why there is a universe at all. For a similar reason . . . science cannot explain why there are the most basic laws of nature that there are’.⁶ The implied conclusion is that we must resort to a supernatural agency to explain the existence and basic laws of a universe. In addition to contradicting this assumption, I also wish to accomplish a second aim, namely, to construct naturalistic explanations of our universe that are not only logically possible but also approximately empirically possible. This will increase the interest and contemporary scientific relevance of the explanations and will enable us to take seriously the suggestion that our universe might, in fact, have explanations of this sort.

My neo I-S explanations require preliminary definitions of a universe, spatial-temporal positions and relations, and basic laws of a universe; the construction of these definitions will occupy us in this section and their employment in the neo-I-S explanations in the next section. Many different definitions are possible and I shall select the definitions that allow for the sort of cosmological explanations in which I am interested. I shall impose a further restriction on my definitions in order to increase the interest of my explanations, that the definitions violate none of the concepts or principles of contemporary cosmological theories. This restriction will enable the neo-I-S explanations offered in section 3 to approximate with a reasonable degree of closeness empirically possible explanations.

I begin with the definition of a universe.

(D1) U is a universe = Df. U is a spacetime such that (i) every spatiotemporal position in U is spatiotemporally related to every other position in U and (ii) there is no spatiotemporal position that is spatiotemporally related to any position in U that is not itself a part of U.

On the face of it D1 allows there to be many universes, since it is possible for there to be two universes U₀ and U₁ such that no spatiotemporal position in U₀ is spatiotemporally related to any position in U₁. This possibility will be essential to my cosmological explanations, which will make reference to many universes.

But D1 remains fundamentally ambiguous until its key expressions, ‘spatiotemporal position’ and ‘spatiotemporally related’ are defined. The former is defined as follows.

D2 P is a spatiotemporal position = Df. P is a point in three dimensional space at an instant of time such that (i) the point has zero spatial volume and the instant zero duration, (ii) between any two spatial points there is a nondenumerable infinity of other spatial points and between any two instants there is a nondenumerable infinity of other instants, (iii) P is irreducible to actual or possible events (an event = an instantaneous temporal part in the history of a point mass or pointlike light ray) and may exist even if no event occupies it.

Condition (iii) commits me to a ‘substantivalist’ rather than ‘relational’ theory of spacetime and thus sides me with Earman, Nerlich, Friedman and others.⁷ The substantivalism I assume allows that there may be empty spacetimes, such as an empty Minkowski spacetime or an empty de Sitter spacetime, but nothing important in my explanations hinges on this contention and I mention it only to decrease the vagueness of the spacetime notions I shall be employing.

If two spatiotemporal positions are to belong to the same universe, then they must be spatiotemporally related. The definition of spatiotemporal relatedness will be crucial to my explanations and some care must be taken in choosing the appropriate definitions. It might seem at first blush that the timelike, spacelike and lightlike relations defined in standard treatments of the Special Theory of Relativity (STR) would suffice for my purposes. For example, it might be said that two spatiotemporal positions belong to the same universe if they are spacelike related (‘topologically simultaneous’) and that two positions are spacelike related if and only if it is impossible for them to be occupied by events that are connected by light or slower signals. But this definition is unsuitable for my purposes, since two events E₀ and E₁ that occupy two spatially disconnected universes are unconnectible by light or slower signals and yet I do not want to say the positions they occupy are spatiotemporally related.

If I add to the definition of spacelike relatedness the condition that the two events are simultaneous or successive relative to some reference frame, I will solve the above problem but a new one will take its place. Two events are simultaneous or successive relative to some reference frame R if and only if it is possible for light signals sent from them to arrive simultaneously or successively at the midpoint between the places occupied by the two events as measured from the perspective of R. A place M is the midpoint between the places occupied by the two events relative to R if and only if R is at rest relatively to M and it is possible to send light signals simultaneously from M to the two places and for these signals to rearrive at M simultaneously. This entails that two events are spacelike related only if they belong to the same spatially continuous universe, since two events in two spatially disconnected universes cannot emit light signals that intersect at a midpoint between the places the two events occupy. Unfortunately, however, this definition is too restrictive for my purposes since it divides into a number of different universes spacetimes that I wish to treat as one universe. Suppose that a spacetime has negative curvature (the spacetime is hyperbolic and ever expanding) and contains two galaxies receding from one another at a combined velocity greater than that of light.⁸ An event E₂ on one galaxy cannot be timelike or lightlike related to an event E₃ on the other galaxy since no signal at or below the velocity of light can connect them. But they cannot be spacelike related either, at least not if the above modified definition is adopted. To be spacelike related, there must be a midpoint between the places occupied by two events relative to a reference frame R. But something is a midpoint M between the two places relative to R only if it is possible to send light signals simultaneously from M to the two places and for these signals to rearrive simultaneously at M. If the two galaxies at which the two events E₂ and E₃ are located are receding from each other at a combined velocity greater than the speed of light, then there is no place M from which signals could be sent simultaneously to both galaxies such that the signals would rearrive at M. It would follow that E₂ and E₃ are not spacelike related and therefore belong to different universes, which is not the result I wish.

There is, however, a definition of spatiotemporal relatedness, based on the General Theory of Relativity (GTR), that is suitable to my purposes. The relations in question are constitutive of cosmic time and I shall call them relations of cosmic simultaneity and cosmic succession. Definitions of these relations require antecedent definitions of a ‘surface of simultaneity’ and a ‘spacelike hypersurface’.

(D3) S is a surface of simultaneity of a local Lorentz frame F at t₁ =df. S is the best of all and only those spatiotemporal positions related to F at t₁ by the relation SIM. Any position P stands in SIM to F at t₁ if and only if F is a world line of a possible observer and t₀, t₁ and t₂ are successive times on F such that (i) it is possible for a light signal to be sent from F at t₀ to P and rearrive at F at t₂, and (ii) the time delta-t elapsed between the emission of the signal from F at t₀ and the rearrival of the signal at F at t₂ obeys the equality delta-t/2 = the temporal distance from t₀ to t₁, = the temporal distance from t₁ to t₂.

(D4) H is a spacelike hypersurface = df. (i) H has three spatial dimensions and is temporally instantaneous; (ii) H is the set of interlocking surfaces of simultaneity of the spatiotemporal positions P₀, P₁, . . . P_n, where each P is different local Lorentz frame at a certain instant; (iii) Each of the positions P₀, P₁, . . . P_n is assigned the same value f(P) by the function f from the spacetime U of which H is a hypersurface to the reals, the function f being such that it increases along every future-directed timelike or lightlike curve of U.⁹

We now can define cosmic simultaneity and cosmic succession:

(D5) The spatiotemporal positions P1 and P2 are cosmically simultaneous = df. (i) P₁ and P₂ cannot be occupied by events that are connected by light or slower signals; (ii) P₁‘s surface of simultaneity coincides locally with the same spacelike hypersurface with which P₂‘s surface of simultaneity coincides locally; (iii) the function f assigns the same value f(P) to P₁ and P₂.

(D6) The spatiotemporal position P₃ is cosmically later than the spatiotemporal position P₂ = df. (i) P₃ can be occupied by an event that is an effect of an event occupying either P₂ or a position cosmically simultaneously with P₂; (ii) P₃‘s past-directed light cone is intersected by a segment of some spacelike hypersurface with which P₂‘s surface of simultaneity coincides locally; (iii) P₂‘s future-directed light cone is intersected by a segment of the spacelike hypersurface with which P₃‘s surface of simultaneity coincides locally; (iv) the function f assigns a higher value f(P) to P₃ than to P₂.

The definition of being cosmically earlier is the inverse of D6 and need not be given. A diagram should render the definitions D3-D6 more intuitively comprehensible:

A, B and C are world lines of possible observers. E₁ is an event that occurs at the spacetime position A at t₁ and E₂ is an event that occurs at the position B at t₁. E₁ and E₂ are cosmically simultaneous; they occur on the same spacelike hypersurface t₁ and the position they occupy is assigned the same value by the function f (which is reflected in the numeral 1 in the designation ‘t₁‘ for the hypersurface to which they belong). The segment of the hypersurface t₁ depicted in the diagram consists of the interlocking surfaces of simultaneity of the positions at which E₁, E₂ are located and of the position C at t₁. The interlocking of the surfaces of simultaneity of the positions at which E₁ and E₂ are located may be taken to imply that a light signal sent from A at t₀ will reflect off E₂ and rearrive at A at t₂, (with the equality described in D3 being satisfied) and that the same holds for a light signal sent from B at t₀ to E_l.

Definitions D3-D6 require spacetime to satisfy certain technical conditions,¹⁰ which may be intuitively summarized by saying that spacetime has a past and future direction and that time travel into the past is impossible.

It must be emphasized that the cosmic time here defined is relative to a way of dividing the spacetime into spacelike hypersurfaces (technically, ‘foliating’ the spacetime into ‘leaves’). There are an infinite number of different ways of foliating the spacetime, each resulting in a different temporal ordering of the spacetime positions, and there is no intrinsic or ‘right’ way to foliate the spacetime. But in some cases there is a simplest way. If a universe is isotropic (looks the same in all directions from any given point) and homogeneous (matter is evenly distributed), then the simplest foliation results from identifying each hypersurface with a plane of homogeneity. At each event on the plane the density and pressure of matter and the curvature of spacetime is the same.¹¹ Our universe is (approximately) isotropic and homogeneous and so there is a privileged cosmic temporal ordering in the sense of a simplest ordering, but I shall allow many of the universes I discuss in Section III to be inhomogeneous and anisotropic.

Cosmic time as defined in D5 and D6 resolves the two problems we found with the two STR-based definitions and spatiotemporal relations. The first definition involved the association of spacelike relatedness (topological simultaneity) with the impossibility of connectedness via light or slower signals; that is, it identified spacelike relatedness with D5, i. This definition was problematic since it entailed that two events in disconnected universes are spatiotemporally related. D5 solves this problem by adding conditions (ii) and (iii) to the condition (i) of spacelike relatedness; these added conditions entail that causally unconnectible events in disconnected universes are not spatiotemporally related via simultaneity since there is no spacelike hypersurface with which the surfaces of simultaneity of the positions of both events coincide. D5 and D6 also solve the problem with the second STR-based definition of spacelike relatedness, which added to D5, i the condition that there is some midpoint between the places of the two events at which light signals from the two events could arrive. This posed a problem in that events in two galaxies receding from each other at a combined velocity greater than that of light would be spatiotemporally unrelated and thus belong to different universes. D5 and D6 solve this problem since if there is no midpoint between the places of the two events (in the sense relevant to the argument) the two events will still be spatiotemporally related since either there is some hypersurface H with which their surfaces of simultaneity both coincide or with which one of their surfaces coincide and which intersects the past/future light cone of the other place. Note that D6, i does not imply that P₃ is later than P₂ only if P₃ can be occupied by an event that is an effect of an event occupying P₂. This would reintroduce our original problem, for if P₃ and P₂ are located at two galaxies receding at a combined velocity greater than that of light and they are not on the same hypersurface then they would be spatiotemporally unrelated, since a light signal could not be sent from one to the other. D6, i instead implies that P₃ is later than P₂ only if P₃ can be occupied by an event that is an effect of an event occupying either P2 or a spatiotemporal position cosmically simultaneous with P₂. Manifestly, there is a position cosmically simultaneous with P₂ that is located within P₃‘s past light cone, even if P₂ is not.

The last definition we need for our cosmological explanations involves the phrase ‘a basic law of a universe’:

(D7) L is a basic law of a universe U = Df. (i) L explains other laws of U but is not itself explained by other laws of U, and (ii) L does not obtain in all universes if there is more than one universe.

An example of a basic law of a universe is

(L₁) For any x, if x is a light signal, then x travels in a vacuum at 186,000 miles per second.

If L₁ is a basic law of a universe U₀ there is no contradiction in supposing that there is another universe U₁ in which L₁ does not hold and in which L₂ holds instead:

(L₂) For any x, if x is a light signal, then x travels in a vacuum at 185,000 miles per second.

However, if a law L explains and is not explained by other laws of a certain universe U, and obtains in every universe (assuming there is more than one universe) then L is not a basic law of a universe. I shall call it instead a ‘metalaw’. The expression ‘other laws of U’ in D7, i refers to laws applying to U other than metalaws.

Suppose there is a universe U₁ very much like our own and that due to an intense gravitational field associated with a collapsing star in one of its regions the world lines of particles and light rays in that region converge and terminate in a singularity. I shall call this singularity a ‘black hole singularity’. The singularity is not a part of the universe U₁ since it neither is a part of nor occupies any of the spacelike hypersurfaces the sequence of which comprises U₁. The singularity is a zero-volume point but it does not have three spatial coordinates and therefore is not a point in the 3D space of U₁. It also does not have a temporal coordinate and for this reason also it is not a position or an occupant of a position in the 4D spacetime of U₁. Rather, it is a boundary or edge of the 4D spacetime of U₁, a point where some of the timelike and null curves in U₁ come to an end.¹²

Let us call this singularity S and suppose that S is not only a boundary of U₁ but a boundary between U₁ and another universe U₀. S is an endpoint of some timelike and null curves in U₁ but a beginningpoint of the timelike and null curves in U₀. In respect of its property as an endpoint of some curves in U₁, S is a ‘black hole singularity’ but in respect of its property as a beginning point of the curves in U₀ S is a ‘big bang singularity’. A diagram will enable this scenario to be described more exactly:

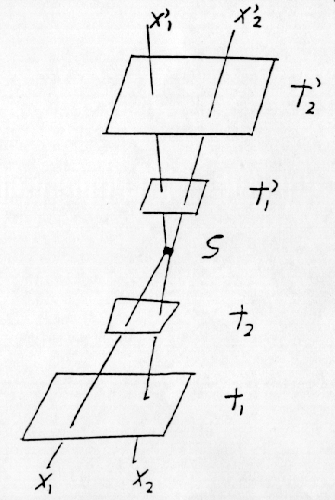
The bottom two rectangles represent a small contracting region R of two successive spacelike hypersurfaces of U₁, with t₂ being later than t₁. The spatially three dimensional region R (the region of the collapsing star) contracts until it is ‘crushed out of existence’ at the singularity S. which is not a spatially three dimensional region but a spatially zero dimensional singular point. X₁ and x₂ are world lines of particles involved in the collapse of the star and these lines end at S, where the particles cease to exist. The top two rectangles represent the universe U₀ in the early phase of its existence. The region of space constituting the spacelike hypersurface t’₁ of U₀ is involved in a big bang explosion and expands, becoming the larger region constituting the later hypersurface t’₂. X’₁ and x’₂ are world lines of particles involved in the big bang explosion.

If U₀ is to count as a distinct universe from U₁, which is a necessary condition of the development of my cosmological explanations, then none of the spatiotemporal positions in U₀ can be related to any of the spatiotemporal positions in U₁. This will be the case only if it is not true both that S is cosmically later than x₁ at t₂ (or any other position in U₁) and cosmically earlier than x’₁ at t’₁ (or any other position in U₀). That this is not true can be proven on the basis of definitions D2-D6. S is cosmically later than x₁ at t₂ only if S has a surface of simultaneity which coincides locally with a spacelike hypersurface H, such that a segment of H intersects the future light cone of x₁ at t₂. But S has no surface of simultaneity that coincides locally with a spacelike hypersurface H since S does not have three spatial coordinates and three coordinates is a necessary condition of possessing such a surface (see D2-D4). For similar reasons, S is not cosmically earlier than x’₁ at t’₁. Moreover, since the future light cone of x_l at t₂ ends at S (is inextendible beyond S), any light signal capable of being sent from x₁ at t₂ terminates at S; this entails that x₁ at t₂ is not cosmically earlier than x’₁ at t’₁, since this relationship between them would require that the future light cone of x₁ at t₂ extend to and intersect the hypersurface to which x’₁ at t’₁ belongs. And these two spatiotemporal positions are not cosmically simultaneous, since they do not belong to any common spacelike hypersurface; they cannot belong to a common one since no hypersurface is extendible through the singularity S, regardless of which way U₀ and U₁ are foliated into different spacelike hypersurfaces.

Since S is neither cosmically later, earlier nor simultaneous with any position in U₀ or U₁, it follows, according to my definition of spatiotemporal relatedness, that S is spatiotemporally unrelated to the positions in both U₀ and U₁. S instead bears to these positions the relation of () being a spatiotemporal boundary of (). More exactly, S bears to the relevant positions in U₁, such as x₁ at t₂, the relation of () being the future boundary of (). S is a future boundary of x_l at t₂ if and only if no future directed timelike or null curve extended from x₁ at t₂ is extendible beyond S. S is a past boundary of x’₁ at t’₁ if and only if no past-directed timelike or null curve extended from x’₁ at t’₁ is extendible beyond S.

The result that the positions in U₀ are spatiotemporally unrelated to the positions in U₁, and hence that U₀ and U₁ are distinct universes in the sense of D1, enables us to develop a cosmological scenario that allows for a neo-I-S explanation of the existence of U₀. Suppose that there are 10 billion black hole singularities that bound different regions of U₁ but that only one billion of these singularities also have the property of being big bang singularities that are past boundaries of other universes. In the other nine billion cases, the black hole singularities are not associated with the ‘birth’ of another universe. Given this, the existence of the universe U₀ can be provided with the following neo-I-S explanation, where ‘U’ expresses the property of () being a big bang singularity that is the past boundary of a universe and ‘B’ expresses the property of () being a black hole singularity that is the future boundary of a region of a universe.

(1) P (U/B) = .10

(2) Bx

__________

__________ [.10]

(3) Ux

If ‘x’ stands for the big bang singularity that is the past boundary of our universe, then (1)-(3) gives an answer to the question ‘Why does our universe exist?’ by providing a neo-inductive-statistical explanation of our universe’s existence. Our universe U₀ exists because there is a black hole singularity Bx bounding another universe U₁ and ten percent of U₁‘s black hole singularities are also big bang singularities that are past boundaries of other universes. A further analysis of explanations of this sort will be given in the following sections, but first let us develop our cosmological scenario so as to provide a neo-I-S explanation of the basic laws of our universe U₀.

It is arguable that the following laws L1-L4 are basic laws of our universe; these laws describe the strength of the four forces relative to the strong force (set at one):

Ll: For any x, if x is a strong force, then x has the value 1.

L2: For any x, if x is an electromagnetic force, then x has the value 1/137.

L3: For any x, if x is a weak force, then x has the value 10^-5.

L4: For any x, if x is a gravitational force, then x has the value 6 x 10^-39

These laws are basic in that they (a) explain other laws of our universe but are not explained by any other laws of our universe, (b) do not obtain in all universes if there are more than one universe.

Let us accept the speculation of many physicists that the first interval of Planck length (10^-43 second) of the big bang explosion of our universe is occupied only by superparticles interacting by means of the superforce. Following this interval and before the end of the first interval of 10^-4 second the superparticles become differentiated into the various types of hadrons (e.g. quarks) and leptons (e.g. electrons) and the superforce becomes differentiated into the gravitational, strong, weak and electromagnetic forces.

This differentiation occurs through symmetry breaking, which occurs in chance or random ways. The chance ways in which the symmetry is broken determine the values of the basic physical constants. In our universe, the symmetry breaks in such a way that the forces acquire such values as the value 0.511 MeV for the mass of the electron.

Since the symmetry breaks in chance ways, it is to be expected that if the same initial conditions at the Planck era obtain in different universes then the values of the basic constants will be settled in different ways in different universes. Suppose there is another universe U’₀ that is past-bounded by a singularity that future-bounds a part of U₁ and that in U’₀ the first Planck-length interval consists of superparticles interacting via the superforce. Subsequent to this interval, the symmetries break in random ways and the four forces and the elementry particles emerge with different values than they possess in our universe. In U’₀ we may say, the strong force is greater by 2% than its value in our universe U₀ and consequently quarks do not combine into protons and no atoms (and thus no stars and galaxies) are formed. Other values obtain in other universes that are past-bounded by singularities that future-bound parts of U₁. Let us suppose that of the ten billion black holes in U₁, two hundred of them are past boundaries of universes that have the same basic laws (including Ll-L4) as our universe U₀. In these two hundred universes, the symmetry present in the interaction of the superparticles via the superforce breaks in a way that results in values of the four forces and elementary particles that are identical with their values in our universe. This allows for a neo-I-S explanation of the basic laws of our universe U₀. As before, let B express the property () being a black hole singularity that is the future boundary of a region of a universe. Let L express the property () being a big bang singularity that is the past boundary of a universe with the set S₀ of basic laws, where S₀ is the set of all and only those basic laws that obtain in U₀. Thus we have

(4) P (L/B) = .00000002

(5) Bx

__________

__________ [.00000002]

(6) Lx

If x stands for the singularity that is the past boundary of our universe U₀ then (4)-(6) explains why our universe has the set S₀ of basic laws rather than some other set. The reason is that x is a black hole singularity in the universe U₁ and .00000002 of U₁‘s black hole singularities are past boundaries of universes that obey the set of basic laws S₀.

I should observe that there are laws governing symmetry breaking and that statistically explain the obtaining of the basic laws Ll-L4 but that (in my scenario) these laws obtain in all universes and therefore are metalaws rather than basic laws of our universe. Thus, my earlier statement that L1-L4 are not explained by other laws of our universe (i.e. by any law applying to our universe but a metalaw) is not vitiated by the explanation of L1-L4 by the laws of symmetry breaking.

A neo-I-S explanation of the initial conditions of our universe, such as the amount of mass-energy initially present in it, can also be given but its construction should be obvious given the above considerations and I will not pause to give it here. Instead, I shall pass to the more interesting task of showing how the cosmological scenario envisaged can be developed so as to provide explanations of the existence of every universe and set of basic laws that is postulated or implied in the explanations. This is desirable, since the explanations (1)-(3) and (4)-(6) explain our universe U₀ only at the price of introducing another universe U₁ as an unexplained given. The existence and basic laws of U₁ can be explained along the lines of (1)-(3) and (4)-(6) if we suppose that U₁ also began in a big bang explosion and that the singularity that is the past boundary of U₁ is the future boundary of a black hole region of another universe U₂. If we suppose that ten percent of U₂‘s black holes are associated with singularities that are past boundaries of other universes, then the explanation (1)-(3) will also explain the existence of U₁. assuming that ‘Bx’ is taken to refer to the black hole singularity in U₂ that is associated with U₁. Further, if we suppose that U₁ obeys the set S₁ of basic laws and that .00000002 of U₂‘s black holes are associated with universes obeying S₁, then (4)-(6) will explain the basic laws of U₁, with a suitable reinterpretation of ‘L’. The existence and basic laws of U₂ can be explained along similar lines, in terms of another universe U₃. U₃ can be explained similarly in terms of U₄ and so on without end. The only constraint is that each of these universes have basic laws (and initial conditions) that permit the formation of black holes; universes that have laws or initial conditions that do not permit their formation can be formed from universes in the series U₁, U₂, U₃, . . . U_n . . . but they are ‘dead ends’ in the line of universes and are not partly bounded by black hole singularities associated with other universes.

In the scenario we are envisaging there is no universe that exists unexplained and no set of basic laws whose obtaining is unexplained. Our ultimate ‘brute facts’ are not the existence of a universe or the obtaining of a set of basic laws of a universe but the existence of an infinite series of universes and the obtaining of the metalaws common to every universe in the series. There is a reason (explanation) why each universe in the series exists but no reason why this infinite series of universes exists rather than some other series or no series at all. And there is a reason why each universe obeys the set of basic laws it in fact obeys, but we do not know why all the universes obey the set of metalaws they all in fact obey rather than some other set or why there are metalaws and laws that are obeyed at all. As before, there still are limits or stopping points of naturalistic explanation but these stopping points are pushed back further than hitherto thought possible, from the existence and basic laws of our universe to the existence and metalaws of an infinite series of universes.

It remains to show that the model of naturalistic explanations involved in these explanations is acausal (section 4) and that the cosmological scenario envisaged is approximately empirically possible and the best candidate currently available for a naturalistic account our universe exists and obeys its basic laws (section 5).

The model used in the explanations in the last section is the neo-I-S model, which explains the existence and basic laws of our universe by subsuming them under statistical laws and thereby providing them with a nomic expectability of some degree. Are the statistical laws used in these explanations reflections of underlying causal regularities and, if not, are the statistical subsumptions (1)-(3) and (4)-(6) thereby devoid of significant explanatory value?

This issue can be made more precise in terms of the theory of causality Salmon develops in Scientific Explanation and the Causal Structure of the World. In this work Salmon articulates a notion of probabilistic causality that he argues to underlie all genuine statistical explanations. (Subsequent page number references in this section refer to this book.) Salmon distinguishes between causal propagation and causal production (p. 139).

Causal propagation is defined in terms of a causal process, the latter being the world line of a material body (e.g. a car) or light pulse (e.g. from a distant star) that transmits its own structure from some spacetime position A to a different position B. Spacetime positions are understood here in accordance with GTR and STR (pp. 140-141), the latter being a special case of the former, and thus can be interpreted in light of my definitions in section 2 (although Salmon himself does not delve into this subject). A causal process propagates a causal influence from an event at A (the cause) to an event at B (the effect) by transmitting its own structure (or a mark or modification thereof) from A to B. Causal propagation involves a temporal distance between the cause and effect and a continuous spatiotemporal path between the cause and effect along which the causal influence is propagated. (Salmon adopts our usual practice of talking of the cause as earlier than the effect but maintains that strictly speaking the temporal relation is symmetric and that we are entitled only to speak of a temporal separation of the two events [p. 176].) The causal influence propagated is probabilistic; that is, the process carries with it probability distributions for engaging in causal interaction of various types. A causal interaction is an intersection of two or more causal processes that produces a modification in the intersecting processes (p. 171).

Causal production is defined in terms of this causal interaction. The causal interaction is an event C that consists of the intersection of the two (or more) causal processes. This event C produces a change in the two causal processes, a modification or ‘mark’ of the structure of the processes that persists ‘after’ the interaction. These changes are produced simultaneously with C, such that the cause and effect in these interactions do not have a temporal separation.

Let us try to map these causal relations onto our cosmological scenario. Suppose a star reaches its Schwarzschild radius at t₁ in the region R of the universe U₁ and begins to contract rapidly to a black hole singularity. The contraction of the particles and photons of the star may be understood as causal processes, processes that stem from the events x₁ at t₁, x₂ at t1, etc., that consist of the star reaching its Schwarzschild radius. May we say that these causal processes all intersect at S, the point of the black hole singularity? And may we say that this intersection is a causal interaction in which modifications are produced in the causal processes, such that the processes emerge from the interaction with the structure of causal processes involved in a big bang explosion? If we can say this, then we can say that a causal influence is propagated from events at t₁ in the region R of universe U₁ to the singularity S, such that the causal processes that transmit this causal influence carry the probability of .10 for undergoing a causal interaction at S that produces a modification of these causal processes from star-contraction-processes to big-bang-explosion-processes. This will imply that the causal interaction occurring at S, which is an effect of the events in R at t₁, is the cause of the big bang explosion that begins the universe U₀.

This mapping fails since four necessary conditions are not met. First, if the intersection of the causal processes at S is to be an effect of the events in R at t₁, then the intersection must be temporally distant from the events in R at t₁. But they are not temporally distant since they are not related by relations of being cosmically earlier or later. Second, if the intersection of the causal processes at S is to be a causal interaction among the processes, then the intersection must occur at a spatiotemporal position, since causal interactions occur only at spatiotemporal positions. But S is not a spatiotemporal position but a boundary to such positions. Third, if the intersection at S is a cause of the big-bang-explosion-structure of the causal processes that evolve in U₀ then the intersection at S must be temporally distant from the times at which these processes possess this structure. But S is not, since S is spatiotemporally unrelated to the times at which these processes possess this structure. This third reason also shows that the big bang explosion cannot be understood as a ‘conjunctive fork’ (pp. 158-168) whose common cause is the intersection at S of the causal processes originating in R. There is a conjunctive fork only if there are two or more separate effects of the same cause, such that the cause occurs earlier than the effect. But the intersection at S is not a cause of any effect in U₀ since it is not earlier than any event in U₀. Fourth, if the intersection at S is to be a causal interaction whereby modifications are produced in the intersecting causal processes, then the processes must be identifiable (must be ‘the same processes, but modified’) on both sides of the intersection.¹³ This implies they must be world lines of the same material bodies and photons. But the mass-energy of the collapsing star ceases to exist at the singularity (is ‘crushed out of existence’) and the mass-energy that appears on the other side of the singularity is not the mass-energy of the star, merely modified, but new mass-energy that appears ex nihilo with S as its past boundary. Spatially 3D mass-energy cannot pass through a singularity that is spatially 0D and reemerge in the 3D space ‘on the other side’ of the singularity. Indeed, we cannot even literally say that the causal processes of the collapsing star ‘intersect’ at S since intersection (at least in Salmon’s sense) is of spatially 3D processes at a spatially 3D position; all that we can literally say is that S is the spatially 0D point towards which the spatially 3D processes converge and at which they cease to exist (the ‘point at which they converge’ being ‘the point at which they cease to exist as spatially 3D processes’).

I should emphasize that though S is not a part of a universe I regard S as real rather than as a mere idealization (the concept of S is different than S, the instance of the concept). Being part of a spatiotemporally 4D universe is not a necessary condition of existence. There is no contradiction in the idea that there exists a zero volume spatial point that (1) lacks three spatial coordinates, that (2) is not assigned a temporal coordinate f(P) by a function f from 4D spacetime to the reals, and that (3) is a past or future boundary of positions that possess these coordinates. S is a very unusual sort of existent, a physical singularity, at which the laws and coordinates of 4D spacetime break down, but being unusual is not the same thing as being self-contradictory and thus my theory (and contemporary cosmological theories) are not reduced to incoherence by the assumption that there are physical singularities.

‘But is it not incoherent to say that S is real but does not exist in time? How can a spatially 0D point exist timelessly?’ Let me make clear that S does exist timelessly if ‘time’ is used in the sense of my definitions, for S does not exist in cosmic time. One is free to construct some other definition of time if one wishes and say that S exists instantaneously or enduringly in this new sense of ‘time’, but the possibility of constructing such a definition does not impugn my case that S does not exist in cosmic time and eo ipso is a boundary between U₀ and U₁ that makes them two different and spatiotemporally disconnected universes in the sense of my definitions (which, I would add, are not arbitrary but are based on contemporary cosmology).

Let me pass now to some more general considerations pertinent to the issue of the causation of universes. The reason why S or events in U₁ cannot be causes of U₀ are instances of more general principles that rule out a priori the possibility that the existence and basic laws of a universe have a natural causal explanation. There can be no natural event or process C that causes a universe U since C must occupy at least one spatiotemporal position P that is cosmically simultaneous with or earlier than (or ‘temporally distant from’, if we wish to preserve Salmon’s temporally symmetric definition) the position(s) occupied by the event(s) or process(es) it causes, and by virtue of this spatiotemporal relatedness P would be a part of the same universe as the position(s) of C’s effects. This prevents C from causing U to exist or obey its basic laws since it entails that C itself is a part of U and obeys it basic laws. (Note that in conformity with D1 the parts of a universe are said primarily to be spatiotemporal positions and are said derivatively to be the events or processes that occupy these positions.) Now no natural event or process can cause itself (recall that I am operating with [arguably intuitively plausible] definitions of a universe that rule out closed timelike curves; see footnote 10). This implies that at best C can cause all the parts of U but C, which is insufficient for C to cause U since U is caused by C only if the whole of U is caused by C.

Salmon believes that unless statistical relations are underpinned by causal explanations the statistical subsumptions do not provide explanations. If so, the statistical relations between black holes and big bangs do not provide an explanation of the existence of our universe U₀. But there is reason to think, however, that Salmon’s theory of nonexplanatory subsumptions does not apply to our subsumptions (1)-(3) and (4)-(6) involving U₀. Salmon’s argument is based on a division of subsumptions into two classes, the class A of explanatory subsumptions that express causal relations and the class B of nonexplanatory subsumptions that possess two defining characteristics, namely, (B₁) they do not express causal relations and (B₂) they express relations that can be explained causally (pp. 135-136). An example of a subsumption that belongs to class B is the subsumption of a sample of gas under the ideal gas law PV = nRT, which relates the pressure (P), volume (V) and temperature (T) of the gas and indicates how these quantities vary as functions of one another. This law does not express a causal relation but the relations it expresses can be explained causally. An increase in the pressure of the gas might be caused by an increase in temperature (through heating the container of the gas) or by a decrease in volume (through moving a piston connected to the container). However, the acausal subsumptions (1)-(3) and (4)-(6) involving our universe U₀ do not possess all the defining characteristics of class B and therefore not only fall outside of Salmon’s class of causal explanations but also outside of his class of nonexplanatory subsumptions. (1)-(3) and (4)-(6) possess the characteristic B₁ since they do not express causal relations, but they do not possess the characteristic B₂ since the relations they express cannot be explained causally, as the foregoing arguments have shown. Thus, Salmon’s theory of nonexplanatory subsumptions does not provide sufficient justification for the thesis that the subsumptions (1)-(3) and (4)-(6) are nonexplanatory. In the absence of other good arguments that such subsumptions are nonexplanatory, I suggest that we rely on the intuition that they are explanatory and that they form a third class in distinction from classes A and B. namely a class C of acausal explanations. But whether only cosmological explanations such as (1)-(3) and (4)-(6) are members of this class is a difficult issue that is neither necessary nor possible to address here.

I understand this issue to be of the extent to which the situations postulated in my neo-I-S explanations conform to currently accepted scientific laws. This is too large a subject to deal with adequately or with any great precision in the space remaining but a few suggestive comments should deepen the interest and relevance of my explanations. These comments are best made in the context of a brief comparison between my explanations of our universe and those that some other contemporary theories might be alleged to provide. Two of the most relevant contemporary theories are Peter Landsberg’s and John Wheeler’s oscillating models of the universe,¹⁴ according to which the universe undergoes many cycles of expansion and contraction, the present expansion phase belonging to the most recent of these cycles. These two models differ in some respects (e.g. Wheeler’s but not Landsberg’s allows values of the fundamental constants to fluctuate from cycle to cycle) but they are similar in respects pertinent to the present discussion. These two theories might be thought to provide empirically possible explanations of the existence or basic laws of our universe. On Wheeler’s theory, for example, it might be alleged to be possible to form neo-I-S explanations of the present cycle in terms of previous cycles. For example, if the set of basic laws S₀ instantiated in our present cycle were instantiated in .00000002 of the previous cycles then the obtaining of these laws in the present cycle might be subsumed under this statistical law and thereby provided with this degree of nomic expectability. It seems to me, however, that these oscillating models fail to provide empirically possible explanations of the existence or basic laws of our universe for two reasons.

The first reason is that it is logically impossible for them to do so, inasmuch as they do not postulate different universes, in the sense of D1, but successive cycles of one and the same universe. Landsberg and Wheeler both talk of ‘earlier cycles’¹⁵ than the present one and imply that one cycle is spatiotemporally related to the next. Thus, even if the existence, initial conditions or basic laws of our cycle could be explained inductive-statistically or deductive-nomologically in terms of previous cycles that would not amount to an explanation of the existence, initial conditions or basic laws of our universe but merely of one phase in the temporal history of our universe.

The second reason the Wheeler and Landsberg models cannot provide empirically possible explanations of our universe is that these models violate known laws of physics and therefore cannot provide empirically possible explanations at all, even of the alleged ‘present cycle’ of our universe. The Landsberg and Wheeler models violate the Hawking-Penrose singularity theorems. Landsberg and Wheeler both admit that the singularity theorems predict that our universe begins in a singularity and that this singularity disallows any earlier cycles of our universe. But Landsberg and Wheeler declare, on the basis of unclear and unargued for philosophical principles (Nature does not provide us with infinities [such as singularities of infinite densities]’¹⁶ and ‘Physics is by definition that which does go on its eternal way [and thereby bypasses predictions of singularities]’¹⁷), that the universe did not begin in a singularity and therefore that a cyclical universe is possible. But these philosophical dismissals of the singularity theorems are unconvincing, if only for the reason of their excessive vagueness, and do little more than distract attention from the fact that their cosmological models violate the singularity theorems without a physical justification for doing so (such as might be provided by a quantum theory of gravity). Inasmuch as their scenarios violate accepted laws and are not shown to obey instead other, better justified, laws, their scenarios cannot be classified as empirically possible.¹⁸

The theory I outlined approximates an empirically possible theory to a greater degree in this respect since this theory is consistent with the singularity theorems. As I explained in the past two sections, I regard each universe as beginning with a big bang singularity and I disallow any spacetime path to be continued through these singularities or through the black hole singularities. But I do not want to suggest that there exists a currently accepted theory that shows our big bang singularity to be a black hole singularity of another universe. Not only is there is no such theory but there is no known solution of the equations of GTR that shows a singularity of one of these sorts to also be a singularity of the other sort. It is important to note in this regard that the solution implying ‘the Einstein-Rosen bridge’ is not such a solution. The Einstein-Rosen bridge presupposes two disconnected universes, each being partly bounded by a black hole singularity, such that the two singularities become joined and form a nonsingular bridge between the two universes. This differs from my scenario if only for the reason that it does not explain the existence of either universe but merely describes how they can become connected through their black holes.

The cosmological scenario I outlined is nearer to that suggested by a question E. Wigner once asked Wheeler in a panel discussion. ‘Is it possible to imagine the explosion of a black hole. Is that nonsense?’¹⁹ Wheeler responded that ‘Zel’ dovich and Novikov proposed it some years ago-the idea that there are in addition to black holes, white holes, and that they should vomit forth matter the way a black hole sucks in matter.’²⁰ But Wheeler’s response here is mistaken or at least misdirected. White holes are not black holes that explode in big bangs but are retarded pieces of the big bang that act like ‘black holes in reverse’, i.e. they spew forth matter rather than suck it in. It is false that a white hole singularity S also has the property of being a black hole singularity, such that S both sucks in matter (e.g. from a collapsing star) and spews forth matter. The white hole singularity only has the property of spewing forth matter. Therefore, it is not an exploding black hole. Wigner’s vague suggestion is better fleshed out in terms of the scenario I suggested, where one and the same singularity S has the property of sucking in matter (qua black hole singularity) and spewing forth matter (qua big bang singularity). Such singularities are not white hole singularities but are in a class sui generis. But unlike white holes, they are disadvantaged in not (yet?) having been derived as solutions to the equations of GTR.

I would like to close this section by mentioning that a remaining apparent candidate for ’empirically possible explanations of the existence and basic laws of our universe’ are the vacuum fluctuation cosmogonies of Tyron, Gott, Zel’dovich, Atkatz and Pagels, Brout, Englert and Gunzig and others.²¹ These cosmogonies postulate an empty background space from which ‘our universe’ fluctuates in accordance with Heisenberg’s uncertainty equation. These theories might be thought to provide a neo-I-S explanation of the existence and basic laws of our ‘universe’ in that the background space engages in numerous vacuum fluctuations and only a small percentage of these develop into full-scale ‘universes’ and an even smaller percentage into ‘universes’ with our basic laws. Thus the existence of ‘our universe’ might be explained by being provided with a nomic expectability to a degree of ten percent and the obtaining of its basic laws might be explained by being provided with a nomic expectability to a degree of .00000002. These vacuum fluctuation cosmogonies do provide empirically possible explanations, or so at least I have argued,²² but they are not explanations of the existence or basic laws of universes in the sense of D1. What fluctuates is not our universe in the sense of D1 but merely a branch of our universe; the fluctuating branch is spatiotemporally connected to the background space and therefore is a part of the same universe as it. The whole universe, the background space plus all of its branches, is not provided an explanation by these cosmogonies; all that is explained is the existence or basic laws of its branches. Therefore, these explanations are not candidates for explanations of the existence and basic laws of our universe.

These considerations suggest that if we are interested in models of logically possible naturalistic explanations of our universe we must look elsewhere than in the oscillating and vacuum fluctuation cosmological models of contemporary theory. I have offered a cosmological theory in outline that both provides a logically possible natural explanation of the existence and basic laws of our universe (and every other universe) and approximates to a reasonable degree an empirically possible explanation. Although its key component is not derivable (at least as far as is presently known) from the equations of GTR, it is consistent both with the singularity theorems and with other areas of contemporary cosmological thought. For these reasons, I suggest that the types of explanation illustrated in the preceding sections are the ones we should take most seriously when we are contemplating in a naturalistic spirit the mystery of our universe.²³

Marion, Indiana

Received March 1988

Revised June 1988

Endnotes

1. See Carl Hempel, Aspects of Scientific Explanation (New York: Free Press, 1965), pp. 381-393.
2. See Wesley Salmon, with contributions by Richard Jeffrey and James Greeno,Statistical Explanation and Statistical Relevance (Pittsburgh: University of Pittsburgh Press, 1971): Wesley Salmon, Scientific Explanation and the Causal Structure of the World (Princeton: Princeton University Press, 1984), Chapters 2-4; Peter Railton, ‘A Deductive-Nomological Model of Probabilistic Explanation’, Philosophy of Science 45: 206-226 (1978). The example of the tunnelling of the alpha particle is used in Salmon’s first-mentioned book on page 58 and in his second-mentioned book on pages 85-86.
3. Carl Hempel, ‘Nachwort 1976: Neuere Ideen zu den problemen der statistischen Erklarung’, in Hempel’s Aspekte wissenschaftlicher Erklarung (Berlin: Walter de Gruyter, 1977), pp. 98-123. For a pertinent discussion of this essay, see Salmon, Scientific Explanation and the Causal Structure of the World, op. cit., pp. 89-90.
4. For example, it has been argued that Hempel’s requirement of maximal specificity guarantees that all known relevant factors are to be taken into account but not that only relevant factors are to be taken into account, and thereby needs to be supplemented by what Fetzer calls a requirement of strict maximal specificity, which rules out laws that state nomically irrelevant properties. See James Fetzer, Scientific Knowledge (Dordrecht: D. Reidel, 1981), pp. 125-26. Also see Wesley Salmon, Hans Reichenbach: Logical Empiricist (Dordrecht: D. Reidel, 1979), pp. 691-694.
   
   It is also argued that Hempel’s analysis of the partial entailment of the explanandum-statement by the explanans-statements in terms of Carnap’s notion of logical probability provides no nonarbitrary way of assigning the numerical values that would warrant the equality of the value of the partial entailment with the value of the nomological probability. See Wesley Salmon, ‘Partial Entailment as a Basis for Inductive Logic’, in N. Rescher (ed.), Essays in Honour of Carl Hempel (Dordrecht: D. Reidel, 1969), pp. 47-82. Fetzer argues this problem is solved by interpreting partial entailments as logical probabilities in Reichenbach’s sense, which allows their numerical equality with nomological probabilities to be given a deductive justification (as measures of nomic expectability) in lieu of an inductive justification (as measures of evidential support). See Fetzer, op. cit., pp. 127-131 end ‘A Single Case Propensity Theory of Explanation’, Synthese 28: 171-198 (1974).
5. On page 250, note 6 and pages 352-53 of Aspects of Scientific Explanation Hempel says that some D-N explanations are acausal and I assume he holds the same for I-S explanations.
6. Richard Swinburne, The Existence of God (Oxford: Clarendon Press, 1979), p. 286.
7. See John Earman, ‘Who’s Afraid of Absolute Space?’, Australasian Journal of Philosophy 48: 287-319 (1970); Graham Nerlich, The Shape of Space (Cambridge: Cambridge University Press, 1976); Michael Friedman, Foundations of Space-Time Theories (Princeton: Princeton University Press, 1983).
8. For a discussion of such situations, see W. Rindler, ‘Visual Horizons in World Models’, Monthly Notes of the Royal Astronomical Society 116: 662-77 (1956), and Richard Swinburne, Space and Time, 2nd ed. (New York; St. Martin’s Press, 1981), Chapter 13.
9. For a discussion of the cosmic time function f, see S.W. Hawking, ‘The Existence of Cosmic Time Functions’, Proceedings of the Royal Society A 308: 433-35 (1968), and Peter Kroes, Tune: Its Structure and Role in Physical Theories (Dordrecht: D. Riedel, 1985). pp. 14-18.
10. The technical conditions are that spacetime is connected, time-orientable, time-anisotropic, time-linear, achronal, Hausdorff, paracompact, strongly causal, and has a positive-definite metric g+ab and an Alexandrov topology.
11. For a discussion of these planes of homogeneity, see Charles Misner, Kip Thorne, and John Wheeler, Gravitation (New York: W.H. Freeman, 1973), pp. 713-725.
12. The idea that singularities are not parts of 4D spacetime is familiar in contemporary thinking. For example, Robert Geroch and Gary Horowitz write in ‘Global Structure of Spacetimes’, General Relativity, ed. S.W. Hawking and W. Isreal (Cambridge: Cambridge University Press, 1979), pp. 256-57. ‘The key idea of what is now widely accepted as the most fruitful definition of a singular spacetime is the following. General relativity, as it is usually formulated, requires a manifold with a smooth Lorentz metric. This formulation leaves no room for points of the manifold at which the metric is singular. Indeed, it is even hard to see how one could modify the theory to admit such “singular points,” for it is only through the metric that one acquires the ability to identify the individual points of the manifold as events. One cannot isolate, as additional physical events, points at which the metric is badly behaved. In short, it seems to be a necessary part of general relativity that all “singular points” have been excised from the spacetime manifold’.
13. Salmon admits (p. 181) that the processes may also be construed as different processes after the interaction, but suggests that it is at least possible to regard them as the same processes (depending, apparently, on the criteria of identity one uses).
14. See Misner, Thorne and Wheeler, op. cit., pp. 1196-217, and Peter Landsberg, ‘The Beginning and End of the Universe’ in Nigmeegse Studies in De Filosofie van De Natuur En Haar Wetenschappen 4: 77-108 (1985).
15. Misner, Thorne and Wheeler, op. cit., p. 1217.
16. Landsberg, op. cit., p. 84.
17. Misner, Thorne and Wheeler, op. cit., p. 1996.
18. The issue of the empirical possibility of the oscillating universe model is discussed at greater length in Quentin Smith, ‘The Uncaused Beginning of the Universe’, Philosophy of Science 55: 39-57 (1988) and ‘World Ensemble Explanations’, Pacific Philosophical Quarterly 67: 73-86 (1986).
19. See Harry Woolf (ed.) Some Strangeness in the Proportion (Addison-Wesley, 1980), p. 383.
20. Ibid.
21. See E.P. Tyron, ‘Is the Universe a Vacuum Fluctuation’, Nature 246: 396-97 (1973); J.R. Gott, ‘Creation of Open Universes from de Sitter Space’, Nature 295: 304-07 (1982); L.P. Grishchak and Y.B. Zel’dovich, ‘Complete Cosmological Theories’, in M.J. Duff and C.J. Isham (eds.) Quantum Structure of Space and Tune (Cambridge: Cambridge University Press, 1982), pp. 409-22; D. Atkatz and H. Pagels, ‘Origin of the Universe as a Quantum Tunnelling Event’, Physical Review D 25: 2065-073 (1982); R. Brout, F. Englert and E. Gunzig, ‘The Creation of the Universe as a Quantum Phenomenon’, Annals of Physics 115: 78-106 (1978).
22. See Quentin Smith, ‘The Uncaused Beginning of the Universe’, op. cit and ‘World Ensemble Explanations’, op. cit.
    
    In an important recent article, Chris Mortensen has argued that a theory partially modelled on Tyron’s can provide explanations of the existence of our universe. See his ‘Explaining Existence’, Canadian Journal of Philosophy 16: 713-22 (1986). Mortensen argues that if we eliminate the background space the existence of our universe can be given an explanation on the basis of ‘a probabilistic theory of Tyron’s kind’ (p. 715). However, Tyron’s theory uses physical probabilities (relative frequencies or propensities) and it is logically impossible for these probabilities to be used if the background space is eliminated, as I have argued in ‘Explaining the Existence of the Universe’ (mimeograph, 1987). But it seems arguable that Mortensen’s theory might be workable if his probabilities are interpreted instead as logical probabilities or subjective probabilities, although I confess that at this point I cannot see how this suggestion might be concretely fleshed out.
23. I am grateful to a referee for this Journal for stimulating comments on an earlier version of this paper.